Matematika Kelas IV Luas Bangun Datar

Pada muatan pelajaran matematika kelas IV sekolah dasar pada materi bangun datar mempelajari tentang luas dan keliling bangun datar. Pada tulisan ini akan membahas mengenai luas bangun datar. saja. Bangun datar yang dibahas pada tulisan ini hanya bangun segitiga, persegi dan persegi panjang saja. Apa itu luas bangun datar? Luas bangun datar adalah besar daerah yang dibatasi oleh sisi-sisi bangun datar tersebut.

A. Luas Persegi

Persegi adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang dengan membentuk 4 titik sudut yang mana besar setiap sudutnya siku-siku 90 derajat. Persegi memiliki beberapa sifat yaitu memiliki 4 titik sudut yang membentuk sudut siku-siku 90 derajat, emiliki 4 rusuk yang sama panjang, memiliki 2 diagonal yang sama panjang, emiliki 4 simetri lipat dan 4 simetri putar. dan emiliki 4 sumbu simetri.

Jika luas persegi adalah L dan sisi persegi adalah s, maka rumus untuk menentukan luas persegi adalah

L = s x s = s².

Untuk menentukan panjang sisi persegi yang diketahui luasnya adalah mengakar pangkat duakan luas tersebut

s = √ L

Untuk menarik akar-akar kuadrat dapat dilakukan langkah-langkah berikut ini:

Sebagai contoh √225 = ...

Pisahkan setiap dua angka dari belakang (2.25)
Tentukan bilangan kuadrat yang hasilnya paling mendekati angka paling kiri. 1 x 1 = 1, mendekati 2. Tulis 1 sebagai hasil bilangan pertama.
Jumlahkan bilangan hasil yang pertama 1 + 1 = 2
Simpan 2, cari bilangan yang sama sehingga 2 … x … = 125 25 x 5 = 125
Tulis 5 sebagai bilangan hasil yang kedua.
Jadi √225 = 15.

Untuk memudahkan berikut ini beberapa akar kuadrat bilangan.

Akar kuadrat √x	Angka (x)	Akar kuadrat √x	Angka (x)
√1	1	√4	2
√9	3	√16	4
√25	5	√36	6
√49	7	√64	8
√81	9	√100	10
√121	11	√144	12
√169	13	√196	14
√225	15	√256	16
√289	17	√324	18
√361	19	√400	20
√441	21	√484	22
√529	23	√576	24

Ayo Mencoba

1. Tentukan luas persegi berikut ini!

a. Diketahui :
Panjang sisi = 4 satuan
Ditanyakan luas persegi
Jawab :
L = s²
L = 4²
L = 16 satuan

b. Diketahui :
Panjang sisi = 17 cm
Ditanyakan luas persegi?
Jawab :
L = s²
L = 17²
L = 289 cm²

c. Diketahui
Panjang sisi = 23 cm
Ditanyakan luas persegi?
Jawab :
L = s²
L = 23²
L = 529 cm²

2. Tentukan panjang sisi persegi berikut!

a. Diketahui :

Luas persegi = 64 cm²

Ditanyakan panjang sisi?

Jawab

s = √ L
s = √ 64
s = 8 cm

b. Diketahui :

Luas persegi = 196 cm²

Ditanyakan panjang sisi?

Jawab

s = √ L
s = √ 196
s = 14 cm

c. Diketahui :

Luas persegi = 441 cm²

Ditanyakan panjang sisi?

Jawab

s = √ L
s = √ 441
s = 21 cm

3. Jika diketahui keliling sebuah persegi 100 cm, berapakah luas persegi tersebut?

Diketahui:

Keliling persegi = 100 cm

Ditanyakan panjang sisi luas persegi?

Jawab :

Panjang sisi :

K = 4 x s maka

s =	K	=	100	= 25 cm
	4		4

Luas Persegi

L = s²
L = 25²
L = 625 cm²

4. Dua buah persegi mempunyai panjang sisi masing-masing 16 cm dan 26 cm, berapakah selisih luas kedua buah persegi tersebut?

Diketahui

Panjang sisi persegi 1 26 cm

Panjang sisi persegi 2 = 26 cm

Ditanyakan selisih luas persegi?

Jawab :

Selisih Luas

Selisih = Luas 2 - Luas 1
Selisih = s² - s²
Selisih = 26² - 16²
Selisih = 676 - 256
Selisih = 420 cm²
Jadi selisih luas kedua persegi adalah 420 cm²

5. Beni ingin membuat taplak meja berbentuk persegi; dari kain batik. Sisi pada taplak meja tersebut adalah 150 cm. Harga 1 m2 kain batik Rp50.000,00. Berapakah luas kain batik yang dibutuhkan oleh Beni? Jika Beni membawa uang Rp150.000,00, berapakah uang kembalian Beni?

Diketahui:

Sisi Kain = 150 cm = 1,5 m

Harga Kain = Rp50.000,00/ m²

Uang yang Dibawa = Rp150.000,-

Ditanyakan:

Luas kain yang dibutuhkan oleh Beni dan uang kembalian Beni.

Jawab:

1. Luas kain yang dibutuhkan oleh Beni.
L = s²
L = 1,5²
L = 2,25 m²
Jadi, luas kain yang dibutuhkan oleh Beni adalah 2,25 m².

2. Uang kembalian Beni.

Untuk mengetahui uang kembalian Beni, kita harus mengetahui terlebih dahulu harga kain yang harus Beni bayar.

Harga kain = Luas x Rp50.000,00

Harga kain = 2,25 x Rp50.000,00

Harga kain = Rp112.500,00

Maka:

Uang kembalian = Jumlah uang - harga kain
Uang kembalian = Rp150.000,00 - Rp112.500,00
Uang kembalian = Rp47.500,00
Jadi, uang kembalian Beni adalah Rp.47.500,00

B. Luas Persegi Panjang

Persegi panjang merupakan salah satu jenis bangun ruang dua dimensi yang sering kita temukan di kehidupan sehari-hari Persegi panjang adalah bangun datar segi empat yang keempat sudutnya siku-siku dengan sisi yang berhadapan yang sama panjang.

Jika luas persegi panjang adalah L, panjang persegi panjang p dan lebar persegi panjang adalah l, maka rumus untuk menentukan luas persegi panjang adalah

L = p x l

Sedangkan untuk mencari salah satu sisi persegi panjang adalah

p =	L	atau l =	L
	l		p

Ayo Mencoba

1. Tentukan luas bangun datar berikut ini!

a. Diketahui :

Panjang = 8 satuan

Lebar = 4 satuan

Ditanyakan luas bangun?

Jawab :

L = p x l

L = 8 x 4

L = 32 satuan

Jadi luas bangun tersebut adalah 32 satuan

b. Diketahui :

Panjang = 23 cm

Lebar = 10 cm

Ditanyakan luas bangun?

Jawab :

L = p x l

L = 23 x 10

L = 230 cm²

Jadi luas bangun tersebut adalah 230 cm²

c. Untuk menentukan luas dari gabungan dua persegi panjang atau lebih, dihitung satu persatu luas tersebut.

Dikatahui persegi panjang 1

Panjang = 20 cm

Lebar = 30 : 2 = 15 cm

Ditanyakan luas bangun 1?

Jawab :

L = p x l

L = 20 x 15

L = 300 cm²

Jadi luas bangun 1 tersebut adalah 300 cm²

Dikatahui persegi panjang 2

Panjang = 30 : 2 = 15 cm

Lebar = 8 cm

Ditanyakan luas bangun 2?

Jawab :

L = p x l

L = 15 x 8

L = 120 cm²

Jadi luas bangun 2 tersebut adalah 120 cm²

Maka luas gabungan bangun datar adalah 300 cm² + 120 cm² = 420 cm²

2. Tentukan panjang atau lebar persegi panjang berikut!

a. Diketahui :

Luas = 64 cm²

Lebar 4 cm

Ditanyakan panjang persegi panjang?

Jawab :

p =	L	=	64	= 16 cm
	l		4

Jadi panjang persegi panjang adalah 16 cm.

b. Diketahui :

Luas = 187 cm²

Panjang 17 cm

Ditanyakan lebar persegi panjang?

Jawab :

l =	L	=	187	= 11 cm
	p		17

Jadi lebar persegi panjang adalah 11 cm.

c. Diketahui :

Luas = 210 cm²

Panjang 21 cm

Ditanyakan lebar persegi panjang?

Jawab :

l =	L	=	210	= 10 cm
	p		21

Jadi lebar persegi panjang adalah 10 cm.

3. Jika diketahui keliling sebuah persegi panjang 110 cm dan lebarnya 25 cm, berapakah panjang dan luas persegi panjang tersebut?

Diketahui :

Keliling = 110 cm

Lebar = 25 cm

Ditanyakan : panjang persegi dan luas persegi ?

Jawab :

a. Panjang persegi panjang :

p =	K	- l =	110	- 25 = 55 - 25 =30 cm
	2		2

b) Luas persegi panjang = p x l

Luas persegi panjang = 30 x 25

Luas persegi panjang = 750 cm²

4. Persegi panjang A mempunyai panjang 13 cm dan lebar 7 cm, sedangkan persegi panjang B mempunyai panjang 23 cm dan lebar 10 cm, berapakah selisih luas kedua buah persegi panjang tersebut?

Diketahui :

Panjang persegi panjang A = 13 cm

Lebar persegi panjang A= 7 cm

Panjang persegi panjang B = 23 cm

Lebar persegi panjang B= 10 cm

Ditanyakan selisih luas?

Jawab :

Lauas persegi panjang A

L = p x l

L = 13 x 7

L = 91 cm²

Jadi luas persegi panjang A adalah 91 cm²

Lauas persegi panjang B

L = p x l

L = 23 x 10

L = 230 cm²

Jadi luas persegi panjang B adalah 230 cm²

Maka selisih luas adalah 230 - 91= 139 cm²

Jadi, selisih kedua luas persegi panjang tersebut adalah 139 cm²

5. Salah satu tetangga Udin seorang petani. Ia mempunyai tanah berbentuk persegi panjang seluas 416 m². Lebar tanah tersebut 16 m. Berapakah panjang tanah petani? Jika petani hendak menjual tanahnya dengan harga Rp 400.000,00 per m², berapakah uang yang didapat petani?

Diketahui :

Luas tanah = 416 m²

Lebar tanah = 16

Harga tanah = Rp400.000,00 per m²

Ditanya : Panjang tanah nila jual tanah ?

Penyelesaian :

a. Panjang tanah,

p =	L	=	416	=26 m
	l		16

b. Nilai Jual Tanah :

Harga jual = Luas tanah × Harga tanah

Harga jual = 416 × Rp400.000,00

Harga jual = Rp166.400.000,00

Kesimpulannya, uang yang didapat petani jika menjual tanahnya adalah Rp166.400.000,00.

C. Luas Segitiga

Segitiga merupakan bangun datar yang dibatasi dengan adanya tiga buah sisi serta memiliki tiga buah titik sudut. Kemudian untuk alas dari segitiga adalah satu dari sisi suatu bangun segitiga. Lalu untuk tingginya adalah garis yang berbentuk tegak lurus dengan sisi alas dan melewati titik sudut yang saling berhadapan dengan sisi alas

Luas segitiga sama dengan setengah luas persegi panjang. Jika luas adalah L, panjang persegi panjang adalah alas segitiga (a) dan lebar persegi panjang adalah tinggi segitiga (t), maka rumus untuk menentukan luas segitiga adalah

LΔ =	1	x a x t
	2

Posisi sisi alas pada segitiga selalu tegak lurus dengan tingginya. Sedangkan untuk mencari alas segitiga adalah

a =	2 x L
	t

Sedangkan untuk mencari tinggi segitiga dapat menggunakan rumus sebagai berikut :

t =	L
	½ x a

Posisi sisi alas pada segitiga selalu tegak lurus dengan tingginya. Sedangkan untuk mencari alas segitiga adalah

a =	2 x L
	t

Ayo Mencoba

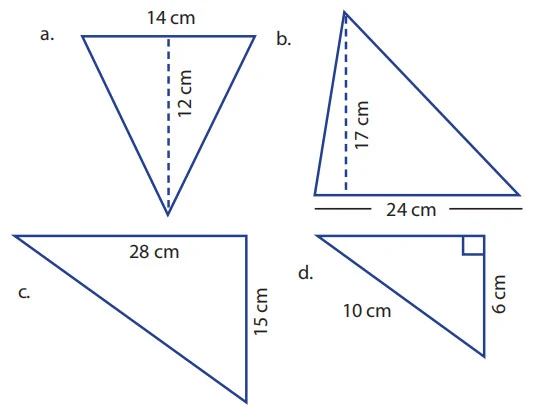
1. Tentukan luas segitiga berikut ini!

a. Diketahui :

Alas segitiga = 14 cm

Tinggi segitiga = 12 cm

Ditanyakan luas?

Jawab :

LΔ =	1	x a x t
	2

LΔ =	1	x 14 x 12
	2

LΔ =	1	x 168 = 84 cm²
	2

b. Diketahui :

Alas segitiga = 24 cm

Tinggi segitiga = 17 cm

Ditanyakan luas?

Jawab :

LΔ =	1	x a x t
	2

LΔ =	1	x 24 x 17
	2

LΔ =	1	x 408 = 204 cm²
	2

c. Diketahui :

Alas segitiga = 15 cm

Tinggi segitiga = 28 cm

Ditanyakan luas?

Jawab :

LΔ =	1	x a x t
	2

LΔ =	1	x 15 x 28
	2

LΔ =	1	x 420 = 210 cm²
	2

d. Diketahui :

Alas segitiga = 6 cm

Tinggi segitiga = 8 cm (gunakan triple pythagoras)

Ditanyakan luas?

Jawab :

LΔ =	1	x a x t
	2

LΔ =	1	x 6 x 8
	2

LΔ =	1	x 48 = 24 cm²
	2

2. Tentukan alas atau tinggi segitiga berikut!

a. Diketahui :

Tinggi 13 cm

Luas = 52 cm²

Ditanyakan alas segitiga?

Jawab :

a =	2 x L
	t

a =	2 x 52	= 104 : 13 = 8 cm
	13

Jadi alas segitiga adalah 8 cm

b. Diketahui :

Alas 25 cm

Luas = 126 cm²

Ditanyakan tinggi segitiga?

Jawab :

t =	L
	½ x a

t =	125	= 125 : 12,5 = 10 cm
	½ x 25

Jadi tinggi segitiga adalah 10 cm

c. Diketahui :

Tinggi 18 cm

Luas = 234 cm²

Ditanyakan alas segitiga?

Jawab :

a =	2 x L
	t

a =	2 x 234	= 468 : 18 = 26 cm
	18

Jadi alas segitiga adalah 26 cm

3. Ayah Edo akan menanam rumput gajah mini pada taman belakang rumahnya yang berbentuk segitiga. Pada taman tersebut sisi terpanjangnya 10 m, sedangkan sisi terpendeknya 6 m. Misalkan harga rumput gajah mini Rp15.000,00 per m², berapakah yang dibutuhkan Ayah Edo untuk menanam rumput gajah mini pada tamannya?

Diketahui :

Sisi miring = 10 m

Alas segitiga = 6 m

Harga rumput gajah mini = Rp15.000,00 / m²

Ditanya :

Biaya yang ayah Edo butuhkan untuk menanam rumput gajah mini ?

Jawab :

Menentukan panjang sisi miring segitiga

Menggunakan teorema phytagoras :

(sisi miring)² = (sisi alas)² + (sisi tegak)²

10² = 6² + (sisi tegak)²

(sisi tegak)² = 10² - 6²

(sisi tegak)² = 100 - 36

(sisi tegak)² = 64

sisi tegak = √64

sisi tegak = 8 m

Menentukan luas segitiga

LΔ =	1	x a x t
	2

LΔ =	1	x 6 x 8
	2

LΔ =	1	x 48 = 24 m²
	2

Menghitung biaya untuk penanaman rumput gajah mini

Harga rumput gajah mini = Rp15.000,00 / m²

Harga rumput gajah mini seluruhnya = Rp15.000,00 x 24

Harga rumput gajah mini seluruhnya = Rp360.000,00

Jadi biaya yang dibutuhkan ayah Edo adalah Rp360.000,00

4. Jika satu batang korek api panjangnya 4 cm, berapakah luas daerah yang dibatasi oleh korek api pada Gambar berikut?

Diketahui :

Alas = 4 x 4 = 16 cm

Tinggi = 4 x 4 = 16 cm

Ditanyakan luas segitiga?

Jawab :

LΔ =	1	x a x t
	2

LΔ =	1	x 16 x 16
	2

LΔ =	1	x 256 = 128 cm²;
	2

Jadi luas segitiga = 128 cm²

Matematika Kelas IV Luas Bangun Datar

0 komentar:

Post a Comment

Please Subscribe

Pencarian

Popular Posts

Labels