Baik pada literasi membaca dan numerasi, kompetensi yang dinilai mencakup keterampilan berpikir logis-sistematis, keterampilan bernalar menggunakan konsep serta pengetahuan yang telah dipelajari, serta keterampilan memilah serta mengolah informasi.
AKM menyajikan masalah-masalah dengan beragam konteks yang diharapkan mampu diselesaikan oleh murid menggunakan kompetensi literasi membaca dan numerasi yang dimilikinya. AKM dimaksudkan untuk mengukur kompetensi secara mendalam, tidak sekedar penguasaan konten. Berikut ini contoh soal AKM numerasi untuk kelas VI Sekolah Dasar.
A. Bilangan
Jika mereka diminta berdiri berurutan dengan nilai terkecil berada di depan, maka tentukan kebenaran pernyataan posisi di bawah ini:
Pernyataan berikut Benar atau Salah?
1. Representasi
a. Memahami bilangan bulat, khususnya bilangan bulat negatif. (4 Soal)
Kompetensi yang diukur :
Memahami bilangan bulat, khususnya bilangan bulat negatif.
Contoh 1 (Pilihan Ganda Kompleks)
Pesawat Terbang
Pada saat terbang pada ketinggian tertentu suhu di dalam pesawat adalah 21° C, sedangkan suhu di luar pesawat 34° C di bawah nol.
Berdasarkan wacana di atas, tentukan Benar atau Salah pernyataan berikut!
| Pernyataan | Benar | Salah |
| Pada saat akan menggambarkan pada garis bilangan, angka 34 terletak di sebelah kiri angka 0 (nol). | Benar | Salah |
| Selisih suhu di dalam pesawat dengan suhu di luar pesawat adalah 13° C. | Benar | Salah |
Pembahasan :
Pada saat akan menggambarkan pada garis bilangan, angka 34 terletak di sebelah kiri angka 0 (nol).(benar)Selisih suhu di dalam pesawat dengan suhu di luar pesawat adalah 13° C. (Salah). 21 - (-34) = 21 + 34 = 55°C
Contoh 2 (Pilihan Ganda)
Pada saat terbang pada ketinggian tertentu suhu di dalam pesawat adalah 21° C, sedangkan suhu di luar pesawat 34° C di bawah nol.
Setiap naik 80 meter, suhu udara di luar pesawat akan turun 0,50° C. Jika ketinggian pesawat naik 2.400 meter, berapakah suhu udara di luar pesawat?
| -15°C |
| -19°C |
| -30°C |
| -49°C |
Pembahasan :
Pada Ketinggian 2.400 Meter => 2.400 M : 80 M = 30Jika setiap Naik 80 Meter suhu turun 0,5°C, Maka pada ketinggian 2.400 Meter :-0,5 x 30 Kali = -15° CelciusJadi Suhu Udara diluar pesawat pada ketinggian 2.400 Meter adalah :-34°C + (-15°C) = -49°C
Contoh 3 (Pilihan Ganda)
Perhatikan gambar termometer berikut!
Sekarang di Belanda sedang musim dingin dengan suhu 10º C. Setelah turun salju, suhunya turun 17 derajat.
Suhu sekarang adalah ….
| -7°C |
| -10°C |
| -17°C |
| -19°C |
Pembahasan :
Suhu sekarang = Suhu awal + Perubahan suhu= 10⁰C + ( - 17⁰C )= 10⁰C - 17⁰C= -7⁰CJadi, suhu di Belanda sekarang adalah -7⁰C
Contoh 4 (Uraian Tertutup)
Perhatikan gambar termometer di atas
Sekarang di Jerman sedang musim dingin dengan suhu -7º C. Setelah turun salju, suhunya turun menjadi -16º C.
Berapakah penurunan suhunya?
Jawaban : 9°C
Pembahasan :
Penurunan suhunya:-7° - (-16°) = -7° + 16° = 9°CJadi, penurunan suhunya sebesar 9°C
b. Menyatakan bilangan desimal dengan dua angka di belakang koma dan persentase dalam bentuk pecahan, atau sebaliknya. (4 Soal)
Kompetensi yang diukur :
Menyatakan bilangan desimal dengan dua angka di belakang koma dan persentase dalam bentuk pecahan, atau sebaliknya.
Contoh 1 (Pilihan Ganda Kompleks)
Perhatikan gambar taman di bawah ini!
Luas taman di halaman belakang sebuah rumah adalah 60 m².
1/6 bagian digunakan untuk kolam.
3/4 bagian untuk rumput dan tanaman lain.
Sisa taman ditutup dengan batu koral.
Tentukan Benar atau Salah pernyataan berikut!
| Pernyataan | Benar | Salah |
| Luas taman yang ditutupi dengan batu koral adalah 5 m² | Benar | Salah |
| Luas taman yang ditutup batu koral lebih luas jika dibandingkan dengan luas taman yang diberi rumput dan tanaman lainnya | Benar | Salah |
Pembahasan :
Luas bagian digunakan untuk kolam = 1/6 x 60 = 10 m²Luas bagian untuk rumput dan tanaman lain = 3/4 x 60 = 45 m²Luas taman yang ditutupi dengan batu koral adalah 5 m². (Benar)Luas taman yang ditutup batu koral lebih luas jika dibandingkan dengan luas taman yang diberi rumput dan tanaman lainnya.(Salah)
Contoh 2 (Pilihan Ganda)
Luas taman di halaman belakang sebuah rumah adalah 58 m².
3/8 bagian taman digunakan untuk kolam.
1/3 bagian untuk rumput dan tanaman lain.
Sisanya ditutup dengan batu koral.
Luas taman yang digunakan untuk kolam adalah ....
| 7,25 m² |
| 16,65 m² |
| 21,75 m² |
| 38,67 m² |
Pembahasan :
Luas koral: =1 - 3/8 - 1/3 =24/24 - 12/24 - 8/24 (kita samakan penyebutnya)Luas koral = 7/24L Kolam = 3/8 × 58 = 21,75 m²L Rumput dan tanaman lain = 1/3 × 58 = 19,33 m²L koral = 7/24 × 58 = 16, 91 m²
Contoh 3 (Uraian Tertutup)
Perhatikan gambar berikut!
Pada label kemasan minuman di atas, dalam 100 mL terdiri dari ... mL sari buah apel.
Pembahasan :
Sari buah apel = 36% x 100 mL = 36 mL
Contoh 4 (Uraian Tertutup)
Jika dituliskan dalam bentuk pecahan paling sederhana, berapakah kandungan sari buah apel?
Jawab : ...
Pembahasan :
36/100 = 36 : 4/100 : 4 = 9/25
c. Mengetahui posisi bilangan desimal dengan dua angka di belakang koma pada garis bilangan serta posisi bilangan bulat termasuk billangan bulat negatif (4 Soal)
Kompetensi yang diukur :
Mengetahui posisi bilangan desimal dengan dua angka di belakang koma pada garis bilangan serta posisi bilangan bulat termasuk billangan bulat negatif
Contoh 1 (Pilihan Ganda Kompleks)
Penilaian Harian
Tabel berikut menunjukkan nilai ulangan matematika dari 5 orang siswa.
| Pernyataan | Benar | Salah |
| Dian berdiri paling depan. | Benar | Salah |
| Titin berdiri paling belakang | Benar | Salah |
| Tepat di depan Wira adalah Tika | Benar | Salah |
Pembahasan :
Urutan nilai dari yang terkecil adalah : (1) Titin, (2) Tika, (3) Wira. (4)Dian, dan (5) AdityaDian berdiri paling depan.(salah)Titin berdiri paling belakang.(salah)Tepat di depan Wira adalah Tika.(Benar)
Contoh 2 (Uraian Tertutup)
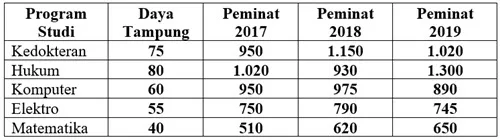
Tabel berikut adalah data daya tampung dan jumlah peminat beberapa jurusan di Perguruan Tinggi A selama tiga tahun terakhir.
Daya tampung dan jumlah peminat berpengaruh dengan tingkat keketatan program studi. Persentase tingkat keketatan program studi dapat dihitung menggunakan rumus 'daya tampung' dibagi 'jumlah peminat' dikali seratus persen. Semakin kecil persentasenya maka semakin besar tingkat keketatannya.
Pada tahun 2017, yang memiliki keketatan tertinggi adalah program studi ...
Pembahasan :
Pada tahun 2017, yang memiliki keketatan tertinggi adalah program studi komputer 60/950 x 100% = 6,31
Contoh 3 (Uraian Tertutup)
Tabel di atas adalah data daya tampung dan jumlah peminat beberapa jurusan di Perguruan Tinggi A selama tiga tahun terakhir.
Daya tampung dan jumlah peminat berpengaruh dengan tingkat keketatan program studi. Persentase tingkat keketatan program studi dapat dihitung menggunakan rumus 'daya tampung' dibagi dengan 'jumlah peminat' dikali seratus persen. Semakin kecil persentasenya maka semakin besar tingkat keketatannya.
Urutan program studi yang memiliki keketatan tertinggi ke keketatan terendah pada tahun 2018 adalah...
Pembahasan :
Komputer, (6,15). Matematika (6,45), Kedokteran (6,52), Elektro (6,96), Hukum (8,60)
Contoh 4 (Uraian Tertutup)
Daya tampung yang disediakan perguruan tinggi untuk penerimaan mahasiswa baru memiliki jumlah yang berbeda-beda di setiap jurusan. Berikut adalah data daya tampung dan jumlah peminat beberapa jurusan di Perguruan Tinggi A tiga tahun terakhir:
Daya tampung dan jumlah peminat berpengaruh dengan tingkat keketatan program studi. Persentase tingkat keketatan program studi dapat dihitung menggunakan rumus 'daya tampung' dibagi dengan 'jumlah peminat' dikali seratus persen. Semakin kecil persentasenya maka makin besar tingkat keketatannya.
Jawablah pertanyaan berikut:
Urutan presentase keketatan program studi matematika mulai dari yang paling ketat adalah
tahun , tahun , tahun
Pembahasan :
2019 (40/650 x 100%=6,15), 2018 (40/620 x 100% =6,45), 2017 (40/510 x 100% =7,84)
2. Sifat Urutan
Mengurutkan beberapa bilangan yang dinyatakan dalam bentuk berbeda. (3 Soal)
Kompetensi yang diukur :
Mengurutkan beberapa bilangan yang dinyatakan dalam bentuk berbeda.
Contoh 1 (Pilihan Ganda)
Budi memegang selembar kertas bertuliskan bilangan 61%.
Dinda memegang selembar kertas bertuliskan bilangan 0,7.
Ade memegang selembar kertas bertuliskan bilangan 0,68.
Yuda memegang selembar kertas bertuliskan bilangan 5/9..
Urutan anak yang memegang kertas bilangan mulai dari yang terkecil berdiri paling depan adalah ....
| A. Yuda, Budi, Ade, Dinda |
| B. Dinda, Yuda, Budi, Ade |
| C. Budi, Dinda, Ade, Yuda |
| D. Yuda, Ade, Dinda, Budi |
Pembahasan :
Budi 61% = 0,61 (2)Dinda 0,7.(4)Ade 0,68.(3)Yuda 5/9 = 0,56 (1)Jadi urutan mulai dari yang terkecil berdiri paling depan Yuda, Budi, Ade, dan Dinda
Contoh 2 (Uraian Tertutup)
Budi memegang selembar kertas bertuliskan bilangan 61%.
Dinda memegang selembar kertas bertuliskan bilangan 0,7.
Ade memegang selembar kertas bertuliskan bilangan 0,68.
dan Yuda memegang selembar kertas bertuliskan bilangan 5/9
Apabila urutan berdiri mulai dari bilangan terbesar, yang berada tepat di belakang Ade adalah ...
Pembahasan :
Urutan berdiri mulai dari bilangan terbesar : Dinda, Ade, Budi, dan Yuda yang berada tepat di belakang Ade adalah Budi.
Contoh 3 (Uraian)
Budi memegang selembar kertas bertuliskan bilangan 61%.
Dinda memegang selembar kertas bertuliskan bilangan 0,7.
Ade memegang selembar kertas bertuliskan bilangan 0,68.
Yuda memegang selembar kertas bertuliskan bilangan 5/9
Dengan urutan berdiri paling depan dari anak yang memegang kertas dengan bilangan terbesar,
Agar Budi berdiri paling depan, kertas siapa sajakah yang bilangannya harus berubah menjadi lebih kecil dari Budi?
Pembahasan :
Kertas yang bilangannya harus berubah menjadi lebih kecil dari Budi adalah Dinda dan Ade
3. Operasi
Menghitung hasil penjumlahan/pengurangan/perkalian/pembagian pecahan atau bilangan desimal, termasuk menghitung kuadrat dan kubik dari suatu bilangan desimal dengan satu angka di belakang komSerta Operasi pada bilangan bulat termasuk bilangan bulat negatif (12 Soal)
Kompetensi yang diukur :
Menghitung hasil penjumlahan/pengurangan/perkalian/pembagian pecahan atau bilangan desimal, termasuk menghitung kuadrat dan kubik dari suatu bilangan desimal dengan satu angka di belakang komSerta Operasi pada bilangan bulat termasuk bilangan bulat negatif
Contoh 1 (Pilihan Ganda Kompleks)
Secara bergantian pesawat-pesawat terbang tinggal landas dan membentuk formasi-formasi tertentu. Pada grup pertama, sebuah pesawat tinggal landas, kemudian grup kedua dengan tiga pesawat yang tinggal landas. Berikutnya grup ketiga dengan lima pesawat yang tinggal landas, kemudian grup keempat dengan tujuh pesawat, seperti terlihat pada tabel.
Tentukan Benar atau Salah pernyataan berikut!
| Pernyataan | Benar | Salah |
| Jika pola penerbangan di atas dilanjutkan, banyak pesawat baru yang diterbangkan pada penerbangan grup ke-6 adalah 11 | Benar | Salah |
| Banyak pesawat yang ada di angkasa setelah penerbangan grup ke-5, bila pesawat-pesawat pada grup-grup sebelumnya belum mendarat adalah 24 | Benar | Salah |
| Hubungan antara grup pesawat dan banyak pesawat yang ada di angkasa adalah “grup pesawat dipangkatkan dua akan sama dengan banyak pesawat di angkasa” | Benar | Salah |
Pembahasan :
Pesawat baru grup ke-6 = 1, 3, 5, 7, 9, 11 (Benar)Pesawat di angkasa grup ke-5 = 1, 4, 9, 16, 25 (Salah)Grup pesawat dipangkatkan dua akan sama dengan banyak pesawat di angkasa (Benar)
Contoh 2 (Uraian)
Terdapat 2 pabrik garmen yang menghasilkan pakaian jadi yaitu pabrik ‘Pada Suka’ dan pabrik ‘Bagus Rapih’. Kedua pabrik tersebut memulai produksinya dari tahun 2014. Banyak produksi pakaian jadi kedua pabrik tersebut disajikan dalam grafik berikut ini.
Pada tahun 2021, kedua pabrik tersebut mendapatkan pesanan 5.000 pakaian. Pabrik manakah yang dapat memenuhi kebutuhan pesanan tersebut? Berikan alasanmu!
Pembahasan :
Pabrik "Bagus Rapih"Pola produksi pabrik "Pada Suka" bertambah 200 per tahun, artinya di tahun 2021 produksinya hanya mencapai 4600.Sementara pola produksi pabrik "Bagus Rapih" bertambah 320, 480, 720, dst. Sehingga produksinya pada tahun 2021 akan mencapai lebih dari 5000.
Contoh 3 (Pilihan ganda)
Banyak pakaian jadi yang diproduksi Pabrik ‘Pada Suka’ di tahun 2024 adalah ….
| A. 4.800 |
| B. 5.000 |
| C. 5.200 |
| D. 5.400 |
| E. 5.600 |
Pembahasan :
Pola produksi pabrik “Pada Suka” bertambah 200 per tahun. Maka pakaian yang diproduksi Pabrik ‘Pada Suka’ pada tahun 2024 adalah 5.200
Contoh 4 (Pilihan Ganda)
Pada tahun 2021 selisih banyak produksi pabrik ‘Pada Suka’ dan ‘Bagus Rapih’ adalah ….
| A. 2.490 |
| B. 2.590 |
| C. 2.690 |
| D. 2.790 |
| E. 2.890 |
Pembahasan :
7.290 - 4.600 -=2.690
Contoh 5 (Uraian Tertutup)
Kincir Ria seperti pada gambar di atas, pertama kali dibangun oleh Ferris Wheel memiliki tinggi 79,5 meter, diameter 75 meter, dan 36 kabin penumpang dengan daya tampung maksimal 2.160 orang. Waktu yang diperlukan kincir ria untuk satu kali putaran adalah 20 menit.
Berdasarkan artikel di atas, jumlah maksimal penumpang dalam satu kabin adalah ... orang
Pembahasan:
Terdapat 36 kabin penumpang dan daya tampung maksimal 2.160 orang, maka Jumlah maksimal per kabin adalah 2160/36 = 60 orang.
Contoh 6 (Uraian Tertutup)
Dalam 3 jam beroperasi, total penumpang yang dapat terangkut oleh kincir ria tersebut adalah ...orang.
Pembahasan:
Dalam 20 menit, mampu mengangkut 2160 orangMaka dalam 1 jam= 60 menit mampu mengangkut 60/20 × 2.160 = 6.480Sehingga dalam waktu 3 jam, dapat mengangkut 3 × 64.800 = 19.440 orang.
Contoh 7 (Uraian Tertutup)
Grafik berikut menunjukkan pencatatan keuangan PT 'Maju Jaya' selama tahun 2019. Tanda negatif menunjukkan kerugian perusahaan dan tanda positif menunjukkan laba yang diperoleh perusahaan.
Dari data tersebut, jumlah uang PT Maju Jaya selama satu tahun adalah ... (ratusan ribu rupiah)
Pembahasan :
6.888 - 3.990 = 2.898
Contoh 8 (Uraian Tertutup)
Persentase kenaikan keuangan terbesar adalah ... % (bilangan bulat)
Contoh 9 (Uraian Tertutup)
Persentase penurunan keuangan terbesar adalah ... % (satu angka di belakang koma)
Contoh 10 (Uraian Tertutup)
Pak Darmo berjualan bubur ayam setiap hari Senin – Jumat dengan modal Rp400.000,00 per hari. Satu porsi bubur ayam dijual Rp10.000,00 dan air mineral Rp4.000,00 per botol. Pada hari Senin sampai dengan hari Kamis 10% keuntungan Pak Darmo disumbangkan untuk Panti Asuhan Maju Bersama, sedangkan pada hari Jumat seluruh keuntungan disumbangkan untuk panti asuhan tersebut.
Jika pada suatu hari Kamis ia menjual bubur ayam 80 porsi dan 30 botol air mineral, maka besar sumbangan ke panti asuhan sebesar ...rupiah
Pembahasan:
Modal : 400.000 rupiahBubur ayam 80 porsi : 80 × 10.000 = 800.00030 botol air mineral : 30 × 4.000 = 120.000Pendapatan hari tersebut : 800.000 + 120.000 = 920.000Keuntungan hari tersebut : 920.000 – 400.000 = 520.000Besar sumbangan ke pantiasuhan adalah 10% × 520.000 = 52.000 rupiah
Contoh 11 (Uraian Tertutup)
Pak Darmo berjualan bubur ayam setiap hari Senin – Jumat dengan modal Rp400.000,00 per hari. Satu porsi bubur ayam dijual Rp10.000,00 dan air mineral Rp4.000,00 per botol. Pada hari Senin sampai dengan hari Kamis 10% keuntungan Pak Darmo disumbangkan untuk Panti Asuhan Maju Bersama, sedangkan pada hari Jumat seluruh keuntungan disumbangkan untuk panti asuhan tersebut.
Berikut adalah data penjualan yang dicatat oleh Pak Darmo selama satu minggu:
Total pendapatan bersih selama satu minggu adalah ... rupiah.
Pembahasan :
1.487.600
Contoh 12 (Uraian Tertutup)
Pak Darmo berjualan bubur ayam setiap hari Senin – Jumat dengan modal Rp400.000,00 per hari. Satu porsi bubur ayam dijual Rp10.000,00 dan air mineral Rp4.000,00 per botol. Pada hari Senin sampai dengan hari Kamis 10% keuntungan Pak Darmo disumbangkan untuk Panti Asuhan Maju Bersama, sedangkan pada hari Jumat seluruh keuntungan disumbangkan untuk panti asuhan tersebut.
Total uang yang disumbangkan selama satu minggu tersebut adalah ... rupiah.
B. Geometri dan Pengukuran
1. Bangun Geometri
Menghitung luas bangun datar (mungkin komposit). (1 Soal)
Kompetensi yang diukur :
Menghitung luas bangun datar (mungkin komposit)
Perhatikan gambar kolam renang berikut!
Kolam renang tersebut berbentuk persegipanjang dengan ukuran panjang 10 meter dan lebar 4 meter yang di sekeliling kolam bagian luarnya dipasang keramik. Jika lebar daerah yang dipasang keramik 50 cm, luas seluruh keramik di sekeliling kolam renang tersebut adalah ....
| A. 15 m² |
| B. 40 m² |
| C. 55 m² |
| D. 64 m² |
Pembahasan :
2((10×0,5)+(4×0,5))2(5+2)14 m²Ditambah 4 sisi4(0,5 × 0,5)4(0,25)1 m²Jadi 14 + 1 = 15 m²
Mengenal limas, kerucut, dan bola (1 Soal)
Kompetensi yang diukur :
Mengenal limas, kerucut, dan bola
(i). Memiliki dua rusuk
(ii). Memiliki lima rusuk
(iii). Memiliki tiga sisi
(iv). Memiliki enam sisi
Di antara pernyataan di atas, yang merupakan pernyataan benar untuk bangun limas segi lima adalah ....
| A. (i) |
| B. (ii) |
| C. (iii) |
| D. (iv) |
Pembahasan :
D (iv)
2. Pengukuran
Mengenal dan menggunakan satuan kecepatan dan debit. (5 Soal)
Kompetensi yang diukur :
Mengenal dan menggunakan satuan kecepatan dan debit.
Contoh 1 (Pilihan Ganda)
Perhatikan gambar berikut!
Volume air yang terbuang seandainya keran air dinyalakan selama setengah menit adalah ....
| A. 0,006 m³ |
| B. 0,003 m³ |
| C. 0,03 m³ |
| D. 3.000 m³ |
Pembahasan :
6 liter per menit, setengan menit = 6 : 2 = 3 liter = 0,003 m³
Contoh 2 (Uraian Tertutup)
Berdasarkan data yang ada, jika keran dinyalakan selama setengah menit, dan air yang terbuang dimasukkan ke dalam gelas berukuran 250 ml, berapa gelas yang diperlukan untuk memuat air tersebut?
Jawaban : ...
Pembahasan :
3 liter : 250 ml = 3.000 : 250 =12 gelas
Contoh 3 (Uraian Tertutup)
Berdasarkan data, berapa cm³/detik debit air yang terbuang dari keran air yang mengalir tersebut? ,,
Pembahasasn :
3.000 ml : 20 detik = 100 cm³/detik
Contoh 4 (Uraian)
Seandainya air yang dibiarkan mengalir selama 1 jam tersebut ditampung di dalam sebuah wadah/ember, wadah/ember manakah yang akan kamu gunakan agar dapat menampung seluruh air tersebut?
A. Wadah/ember berkapasitas lebih dari 350 liter.
B. Wadah/ember berkapasitas kurang dari 350 liter.
Jelaskan dengan perhitungan!
Pembahasan :
A Karena 1 jam = 60 menit, maka volumenya = 60 dikali 6 = 360 liter.
Contoh 5
Terdapat satu keluarga terdiri dari ayah, ibu, dan dua orang anak. Jika setiap anggota keluarga memerlukan 2 liter air per hari untuk minum, setara berapa menitkah air keran yang menyala untuk keperluan minum satu keluarga tersebut?
Jawaban ...
8/6 = 1,33 menit
C. Aljabar
1. Persamaan dan Pertaksamaan
Menyelesaikan persamaan linier 1 variabel (misal 2x + 3 = 7). (8 Soal)
Kompetensi yang diukur :
Menyelesaikan persamaan linier 1 variabel (misal 2x + 3 = 7)
Contoh 1 (Pilihan Ganda)
Di kota A terdapat dua perusahaan pengiriman barang yang letaknya bersebelahan, yaitu "Cepat Kirim" dan "Lancar Jaya". Kedua perusahaan memiliki tarif yang berbeda. Berikut tabel tarif pengiriman barang setiap perusahaan dari kota A.
Kakak akan mengirim barang seberat 15 kg dari kota A ke kota B melalui perusahaan "Lancar Jaya". Berapakah tarif yang harus dibayar Kakak?
| A. Rp47.500,00 |
| B. Rp40.000,00 |
| C Rp32.000,00 |
| D. Rp30.000,00 |
Prmbahasan :
30.000 + (5 x 2.000) = 30.000 + 10.000 = 40.000
Contoh 2 (Uraian Tertutup)
Defi yang tinggal di kota A ingin mengirim barang seberat 12 kg ke kota D. Ia membawa uang Rp50.000,00. Berapa kembalian terbanyak yang akan ia terima?
Jawaban: ...
Pembahasan :
50.000 - (36.000 + 2.000 +2.000) = 50,000 - 40.000 = 10.000
Contoh 3 (Pilihan Ganda Kompleks)
Untuk mempermudah pelanggannya, perusahaan "Cepat Kirim" membuat aplikasi seperti berikut.
Pada hari Rabu, perusahaan "Cepat Kirim" memberikan potongan harga yang sama untuk semua pengiriman. Pada hari itu, Dina melihat biaya pengiriman barang ke rumah neneknya. Pada aplikasi muncul sebagai berikut.
| Pernyataan | Benar | Salah |
| Biaya yang muncul saat Dina menuliskan berat 11 kg dari kota A ke kota B pada hari Senin adalah Rp.41.500,00 | Benar | Salah |
| Pada hari Rabu, Dina mengirim paket ke rumah neneknya dengan berat 17 kg. Biaya yang harus ia bayar adalah Rp.50.500,00 | Benar | Salah |
| Biaya pengiriman paket seberat 16 kg dari kota A ke kota B dengan "Cepat Kirim" pada hari Selasa akan sama dengan biaya pengiriman paket seberat 20 kg pada hari Rabu | Benar | Salah |
Pembahasan :
Biaya yang muncul saat Dina menuliskan berat 11 kg dari kota A ke kota B pada hari Senin adalah Rp.41.500,00.(Benar)Pada hari Rabu, Dina mengirim paket ke rumah neneknya dengan berat 17 kg. Biaya yang harus ia bayar adalah Rp.50.500,00.(Salah)Biaya pengiriman paket seberat 16 kg dari kota A ke kota B dengan "Cepat Kirim" pada hari Selasa akan sama dengan biaya pengiriman paket seberat 20 kg pada hari Rabu.(Salah)
Contoh 4 (Uraian)
Beni tinggal di kota A ingin mengirim paket seberat 20 kg ke kota C, namun ia hanya membawa uang Rp60.000,00. Ia memutuskan untuk kembali ke rumah mengambil uang karena merasa uangnya tidak cukup. Setujukah kamu dengan keputusan Beni? Jelaskan alasanmu! .
Pembahasan :
Tidak SetujuBeni bisa mengirimkan paket tersebut di perusahaan ekspedisi "Cepat Kirim" dengan biaya 56 ribu rupiah
Contoh 5 (Pilihan ganda)
Perhatikan gambar di atas!
Aisyah memarkir sepeda motornya selama 1 jam 30 menit. Biaya parkir yang harus dibayar adalah ....
| A. Rp1.000,00 |
| B. Rp2.000,00 |
| C Rp3.000,00 |
| D. Rp4.000,00 |
Pembahasan :
2.000 + 1.000 = 3.000
Contoh 6 (Pilihan Ganda)
Sebuah mobil diparkir selama 10 jam, biaya parkir yang harus dibayar adalah .…
| A. Rp50.000,00 |
| B Rp45.000,00 |
| C Rp23.000,00 |
| D. Rp10.000,00 |
Pembahasan :
5.000 + (9 x 2,000) = 5.000 +18.000 = 23.000
Contoh 7 (Pilihan Ganda Kompleks)
Manakah dari penyataan di bawah ini yang memungkinkan seseorang membayarkan parkir sebesar Rp9.000,00?
| Memarkir motor selama 8 jam |
| Memarkir mobil selama 3 jam |
| Memarkir motor selama 9 jam |
| Memarkir mobil hampir 2 jam |
| Memarkir motor lebih dari 9 jam |
Pembahasan :
Memarkir motor selama 8 jam = 2.000 + (7 x 1.000) = 2.000 +7.000 = 9.000 (A)Memarkir mobil selama 3 jam = 5.000 + (2 x 2.000) = 5.000 + 4.000 = 9.000 (B)
Contoh 8 (Uraian)
Sebuah motor masuk ke dalam area parkir Stasiun Jakarta Kota pada pukul 09.50 dan keluar pada pukul 18:00. Berapa kembalian yang akan diterima bila ia membayar dengan selembar uang Rp50.000,00?
Jawaban ...
50.000 - (2.000 + (8 x 1.000)) = 50.000 - 10.000 = 40.000
2. Relasi dan Fungsi (termasuk Pola Bilangan)
Menentukan suku ke-n pada suatu pola bilangan sederhana. (1 Soal)
Kompetensi yang diukur :
Menentukan suku ke-n pada suatu pola bilangan sederhana..
Pembahasan :
a = 2b = 2U12 = a + 11b = 2 + 11 (2) = 2 + 22 = 24
3. Rasio dan Proporsi
Menggunakan rasio/skala untuk menentukan nilai/bilangan yang tidak diketahui. (1 Soal)
Kompetensi yang diukur :
Menggunakan rasio/skala untuk menentukan nilai/bilangan yang tidak diketahui
Perhatikan peta berikut!
Diketahui skala peta di atas adalah 1 : 1.250.000. Jika jarak antara kota Gresik dan kota Malang pada peta 8 cm, maka jarak sebenarnya kedua kota tersebut adalah ….
| A 10 km |
| B 50 km |
| C 100 km |
| D 150 km |
Pembahasan :
8 x 12,5 = 100 km
D. Data dan Ketidakpastian
1. Data dan Representasinya
Membaca (= memetik informasi dari) data yang disajikan dalam bentuk tabel, diagram batang, dan diagram lingkaran (termasuk pula cara pengumpulan data dan cara penyajiannya) (3 Soal)
Contoh 1
Data pekerjaan penduduk di suatu wilayah adalah sebagai berikut:
pedagang 200 orang;
PNS 20 orang;
pegawai swasta 80 orang;
dan wiraswasta 100 orang.
Pembahasan :
Pedagang 200/400 = 50%PNS 20/400 = 5%Pegawai swasta 80/400 = 20%Wiraswasta 100/400 = 25%Jawaban A
Contoh 2
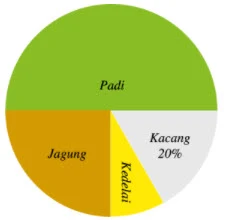
Diagram lingkaran berikut adalah data hasil panen desa Mentari.
Jika jumlah seluruh panen adalah 500 kwintal, berapa kwintal panen jagung?
| A. 250 kwintal |
| B. 125 kwintal |
| C 100 kwintal |
| D. 25 kwintal |
Pembahasan :
Jagung = 25% x 500 = 125 kwintal.
Contoh 3
Diagram lingkaran berikut adalah data kegemaran olahraga siswa kelas VI.
Berapa persenkah siswa yang gemar bulutangkis?
| A. 50% |
| B. 25% |
| C 17% |
| D. 8% |
Pembahasan :
Bulutangkis = 100 % - (Sepakbola 50% + Voli 8% +Futsal 25%) = 100% - 83^ = 17%
































NENI SUMARNI
ReplyDeletesemoga lolos
ReplyDelete