Soal Latihan Materi Bilangan Bulat Kelas VI SD

Mengurutkan bilangan bulat dengan garis bilangandapat dilakukan dengan cara sebagai berikut. Pertama, Letakkan bilangan bulat yang diurutkan pada garis bilangan bulat. Kedua tentukan arah urutan bilangan pada garis bilangan bulat. Arah ke kanan berarti urutan dari terkecil, sedangkan arah ke kiri berarti urutan dari terbesar. Ketiga , tentukan urutan bilangan yang tepat sesuai arah panah pada garis bilangan bulat.

Membandingkan bilangan bulat dengan garis bilangan dapat dilakukan dengan cara sebagai berikut. Pertama. letakkan bilangan bulat yang dibandingkan pada garis bilangan bulat. Kedua, tentukan letak bilangan bulat di sebelah kiri atau di sebelah kanan.

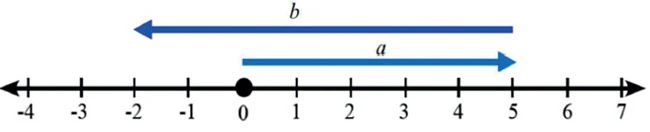
Dalam menghitung hasil penjumlahan dua bilangan bulat, dapat digunakan dengan menggunakan garis bilangan. Bilangan yang dijumlahkan digambarkan dengan anak panah dengan arah sesuai dengan bilangan tersebut. Apabila bilangan positif, anak panah menunjuk ke arah kanan.Sebaliknya, apabila bilangan negatif, anak panah menunjuk ke arah kiri.

Sifat-sifat pada penjumlahan bilangan bulat ada dua (2), yaitu komutatif dan assosiatif. Sifat komutatif adalah sifat pertukaran dua bilangan pada operasi hitung penjumlahan, dimana pengerjaan operasi hitung dua bilangan yang ditukarkan tempatnya tersebut hasilnya sama.

Sifat assosiatif dalam penjumlahan adalah mengelompokkan tiga bilangan atau lebih dengan urutan berbeda. Sifat komutatif disebut juga sifat pertukaran. Penjumlahan dua bilangan bulat selalu diperoleh hasil yang sama walaupun kedua bilangan tersebut dipertukarkan tempatnya.

Seperti pada penjumlahan bilangan bulat, untuk menghitung hasil pengurangan dua bilangan bulat dapat digunakan bantuan garis bilangan. Sifat-sifat operasi hitung pengurangan antara lain sebagai berikut Pengurangan pada bilangan bulat bersifat tidak asosiatif dan pengurangan bilangan bulat tidak komutatif.

Perkalian adalah operasi penjumlahan berulang dengan bilangan yang sama. Operasi perkalian biasanya disimbolkan dengan tanda silang (×) atau tanda titik (∙). Konsep perkalian sesungguhnya berasal dari operasi penjumlahan yang berulang.

Sifat-sifat perkalian bilangan bulat ada tiga (3, yaitu komutatif, assosiatif, dan distributif.). Pada perkalian untuk setiap bilangan bulat a dan b , selalu berlaku = a x b = b x a. Pada perkalian untuk setiap bilangan bulat a, b, dan c selalu berlaku (a x b) x c= a x ( b x c).

.

Sifat distributif perkalian terhadap penjumlahan Untuk setiap bilangan bulat a, b, dan c selalu berlaku = a × (b + c)=(a × b)+(a × c) Sifat distributif perkalian terhadap pengurangan Untuk setiap bilangan bulat a,b , dan c selalu berlaku =a×(b-c)=(a×b)-(a×c)

Invers (lawan atau kebalikan) dari operasi perkalian adalah operasi pembagian. Operasi pembagian biasanya disimbolkan dengan tanda titik dua (÷ atau :) atau tanda garis (/). Lain halnya dengan perkalian, konsep pembagian merupakan pengurangan berulang sampai habis.

Sifat-sifat perkalian bilangan bulat ada tiga (3, yaitu komutatif, assosiatif, dan distributif.). Sifat apa saja yang ada pada pembagian? Pembagian pada bilangan bulat tidaklah berlaku sifat komutatif (pertukaran) serta pembagian pada bilangan bulat tidaklah berlaku sifat Asosiatif (Pengelompokan).

Jawablah pertanyaan berikut dengan tepat!

1. Urutkan bilangan bulat berikut dari yang terbesar!

a. -12, -5, -10, 0, 2, - 2

b. 3, 7, -8, 5, -9, -10

c. -15, 13, -12, 10, 0

d. -7, 7, 1, -1, 12, -11

2. Nyatakan benar atau salah kalimat matematika berikut!

a. -10 < -12 (Salah)

b. -23 < -10 (Benar)

c. 10 < -11 (Salah)

d. 13 > -13 (Benar)

3. Nyatakan operasi yang ditunjukkan garis bilangan berikut dan tentukan hasilnya! (mulai dari 0).

4. Berapakah hasil dari (-10 + 4) x ( -5 – 4)?

5. Berapakah hasil dari -6 + (6 : 2) – ((-3) x 3 )?

6. Hitunglah hasil operasi berikut:

a. (-12 + 17) x 8 + 12

b. 24 x ( -12 ) : 4 - ( -10)

c. 120 : ( -10 ) x 8 + ( -20 )

7. Suhu mula-mula sebuah ruangan periksa, yaitu -5°C. Setelah penghangat ruangan dihidupkan, suhunya naik menjadi 20°C. Berapa besar kenaikan suhu pada ruangan?

Diketahui :

Suhu mula-mula - 5°C

Suhu setelah penghangat ruangan dihidupkan 20°C

Ditanyakan : Berapa besar kenaikan suhu pada ruangan?

Jawab :

= 20 – (–5) 

= 20 + 5 

= 25˚C

Jadi besar kenaikan suhu adalah  25˚C

8. Suhu di daerah Khatulistiwa 28˚C, sedangkan suhu di kutub utara 12˚C di bawah nol. Berapa perbedaan suhu di kedua tempat tersebut?

Diketahui :

Suhu daerah khatulistiwa adalah 28˚C

Suhu di kutub utara 12˚C

Ditanyakan : Berapa perbedaan suhu di kedua tempat tersebut?

Jawab :

= 28 – (–12) 

= 28 + 12 

= 40˚C

Jadi peredaan suhu kedua tempat adalah 40˚C

9. Puncak Gunung Merbabu terletak di ketinggian 250 m. Dangkalan Pahalun letaknya 525 m di bawah puncak Gunung Merbabu. Berapakah ketinggian Dangkalan Pahalun?

10. Diketahui suatu gedung berlantai 12. 3 diantara gedung tersebut berada di bawah permukaan tanah. Udin berada di lantai terbawah, kemudian naik 7 lantai dengan lift. Di lantai berapakah ia berada di atas permukaan tanah?

Diketahui :

Lantai gedung 12, 3 lantai berada di bawah permukaan tanah

Udin dari lantai terbawah naik 7 lantai

Ditanyakan : Di lantai berapakah Udin berada di atas permukaan tanah?

Jawab :

11. Pada perlombaan papan panahan, aturannya sebagai berikut.

Hitam mendapat skor 5.

Kuning mendapat skor 2.

Merah mendapat skor -1.

Biru mendapat skor -3.

Beni membidik 10 kali dengan hasil sebagai berikut. 3 panah mengenai bidang hitam, 2 panah mengenai bidang kuning, 2 panah mengenai bidang bidang merah dan sisanya mengenai bidang biru. Berapakah skor yang diperoleh Beni?

Hitam mendapat skor 5.

Kuning mendapat skor 2.

Merah mendapat skor -1.

Biru mendapat skor -3.

Jadi skor yang diperoleh Beni adalah 8

12. Skor pada kompetisi matematika adalah 4 untuk setiap jawaban yang benar. Selanjutnya, 0 untuk soal yang tidak dijawab dan -1 untuk setiap jawaban salah. Dari 50 soal yang diberikan, Siti tidak menjawab 6 soal dan menjawab salah 5 soal. Berapa skor yang diperoleh Siti?

Diketahui :

Jawaban benar 4

Soal tidak dijawab 0

Jawaban salah -1

Siti dari 50 soal 6 tidak di jawab dan salah 5

Ditanyakan : Berapa skor yang diperoleh Siti?

Jawab "

= ( 6 × 0) + ( 5 × –1) + (39 × 4)

= 0 – 5 + 156

= 151

Jadi skor yang diperoleh Siti adalah 151

13. Ayah Edo mempunyai 75.000 batu bata untuk membangun rumahnya. Setelah dilakukan penghitungan, batu bata yang dibutuhkan rumah 49.670 batu bata. Untuk membuat pagarnya diperlukan 24.600 batu bata. Berapa batu bata lagi yang harus dibeli Ayah Edo?

Diketahui :

Ayah Edo membeli 75.000 batu bata

Kebutuhan batu bata 49.670

Pagar membutuhkan 24.600 bata

Ditanyakan : Berapa batu bata lagi yang harus dibeli Ayah Edo?

Jawab :

= 75.000 – (49.670 + 24.600)

= 75.000 – 74.270

= 730

Jadi batu bata pak Ahmad sisa 730

14. Seorang pedagang mempunyai modal sebesar Rp2.000.000,00. Setelah berjualan, pedagang tersebut mengalami kerugian sebanyak 2 kali masing-masing Rp20.000,00 dan Rp35.000,00. Namun pada penjualan sesudahnya, pedagang mendapat 2 keuntungan masing-masing Rp30.000,00. Berapa rupiah uang pedagang sekarang?