Luas permukaan gabungan adalah menjumlahkan luas sisi terluar. Bagian yang dihitung adalah bagian yang terlihat. sedangkan yang tidak terlihat atau yang berhimpitan tidak dihitung. Menghitung luas permukaan bangun ruang gabungan yaitu jumlahkan sisi tegak (selimut) kedua bangun dengan alas gabungan bangun.
Untuk memudahkan dalam menghitung luas permukaan bangun ruang, berikut ini merupakan tabel rumus luas permukaan beberapa bangun ruang.
| No. | Bangun Ruang | Luas Permukaan |
|---|---|---|
| 1. | Prisma | (2 × La) + (K x t) |
| 2. | Tabung | 2πr(r+t) |
| 3. | Limas | La + Ls |
| 4. | Kerucut | πr (s + r) |
| 5. | Bola | 4πr² |
| 6. | Kubus | 6s² |
| 7. | Balok | 2 ( pl + pt + lt ) |
Beberapa langkah yang perlu dilakukan saat akan menghitung luas permukaan bangun ruang antara lain sebagai berikut.
- Kenali bangun ruang apa saja yang membangun gabungan bangun ruang tersebut.
- Tentukan ukuran-ukuran dari unsur-unsur bangun ruang tersebut.
- Pada bagian yang berimpit biasanya tidak dihitung.
- Hitunglah luas permukaan menggunakan rumus masing-masing permukaan bangun ruang.
Untuk dapat menyelesaikan soal matematika, ikuti langkah-langkah berikut ini.
- Tulis apa yang diketahui.
- Tulis apa yang ditanya.
- Tulis cara penyelesaian.
- Lakukan pengecekan kembali.
- Tulis kesimpulan jawabannya.
Contoh 1
Meli dan Siti akan membuat kerajinan dari flannel. Diameter ice cream tersebut 7 cm. Panjang garis tepi cone 15 cm. Berapa cm² kain flannel yang dibutuhkan?
Diketahui :
Panjang diameter ice cream 7 cm
Diameter bola dan kerucut 7 cm.
Jari-jari bola dan kerucut 3,5 cm
Panjang garis pelukis kerucut 15 cm.
Ditanyakan : Luas kain flanel yang dibutuhkan.
Jawab :
Luas permukaan ice cream sama dengan luas permukaan setengah bola. Jika dihitung hasilnya adalah
| L = | 1 | x 4πr² |
| 2 |
| L = 2 x | 22 | x 3,5 x 3,5 |
| 7 |
L = 44 x 0,5 x 3,5
L = 22 x 3,5
L = 77 cm²
Luas permukaan cone sama dengan luas permukaan selimut kerucut
Ls = πrs
| Ls | 22 | x 3,5 x 15 |
| 7 |
L = 11 x 15
L = 165 cm²
Luas permukaan bangun adalah jumlah dari luas setengah bola dan luas selimut kerucut.
Hasilnya adalah
L = 77 cm² + 165 cm²
L = 242 cm²
Jadi, luas kain flannel yang dibutuhkan adalah 242 cm².
Ayo Mencoba
Meli dan Siti ingin membuat kerajinan tangan seperti di atas. Diameter yang diperlukan 14 cm. Tingginya 20 cm, berapa cm² kain flannel yang dibutuhkan?
Diketahui :
Diameter bola dan kerucut 14 cm.
Jari-jari bola dan kerucut 7 cm.
Tinggi kerajinan 20 cm.
Tinggi kerucut = 20 - 7 = 13 cm
Ditanyakan : Luas kain flanel yang dibutuhkan.
Luas permukaan ice cream sama dengan luas permukaan setengah bola. Jika dihitung hasilnya adalah
| L = | 1 | x 4πr² |
| 2 |
| L = 2 x | 22 | x 7 x 7 |
| 7 |
L = 44 x 0,5 x 7
L = 22 x 7
L = 154 cm²
Hitung panjang garis pelukis (s) kerucut dengan menggunakan cara sebagai berikut :
s² = r² + t²
Keterangan :
s = garis pelukis (cm)
r = jari jari (7 cm)
t = tinggi (20 - 7 = 13 cm)
Maka cara menghitungnya yaitu :
s² = r² + t²
s² = (7 cm)² + (13 cm)²
s² = 49 cm² + 169 cm²
s² = 218 cm²
s = √218 cm²
s = 14,76 cm
Luas permukaan cone sama dengan luas permukaan selimut kerucut
Ls = πrs
| Ls = | 22 | x 7 x 14,76 |
| 7 |
L = 11 x 14,76
L = 162,36 cm²
Luas permukaan bangun adalah jumlah dari luas setengah bola dan luas selimut kerucut.
Hasilnya adalah
L = 154 cm² + 162,36 cm²
L = 316,36 cm²
Jadi, luas kain flannel yang dibutuhkan adalah 316,36 cm².
Contoh 2
Tentukan luas permukaan gambar berikut!
Diketahui :
Rusuk kubus = 8 cm
Sisi miring segitiga = 5 cm
Alas segitiga = 8 : 2 = 4 cm
Ditanyakan : Luas permukaan bangun gabungan.
Pertama cari tinggi segitiga dengan dalil phitagoras
t² = 5² - 4²
t² = √ 25 - 16
t² = √9
t = 3 cm
Luas sisi tegak limas adalah luas keempat sisi tegak yang berbentuk segitiga. Perhitungannya adalah
L = 4 x LΔ
L = 4 x ½ x 8 x 3
L = 2 x 8 x 3
L = 48 cm²
Luas kubus tanpa tutup adalalah luas keempat sisi tegak dan luas alasnya. Perhitungannya adalah
L = 4 s² + s²
L = (4 x 8 x 8) + (8 x 8)
L = 256 + 64
L = 320 cm²
Luas bangun adalah hasil penjumlahan dari luas sisi tegak limas dan luas kubus tanpa tutup.
L = 48cm² +320 cm²
L = 368 cm²
Jadi, luas permukaan bangun di atas adalah 368 cm²
Ayo Mencoba
Kerjakan soal berikut dengan teliti!
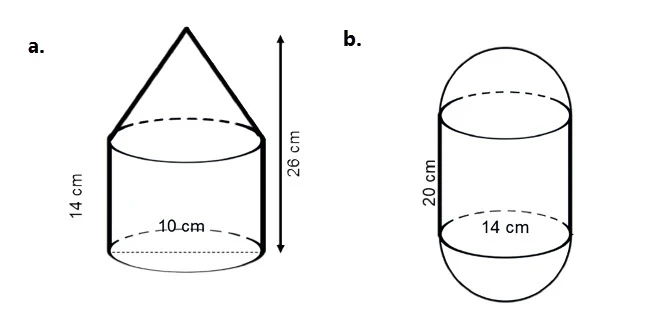
1. Tentukan luas permukaan gambar di bawah ini!
a. Luas Permukaan
Diketahui :
Tinggi tabung = 14 cm
Diameter tabung = 10 cm
Jari-jari tabung = 5 cm
Tinggi kerucut = 26 - 14 = 12 cm
Ditanyakan : Luas permukaan bangun gabungan.
Jawab :
Cari terlebih dahulu sisi miring kerucut dengan dalil phitagoras
s² = r² + t²
s² = 5² + 12²
s² = 25 + 144
s = √169
s = 13
Jadi sisi miring kerucut adalah 13 cm.
Luas gabungan = luas tabung tanpa tutup + selimut kerucut
L = (π x r x r) + (2 x π x r x t) + (π x r x s)
L = (3,14 x 5 x 5) + (2 x 3,14 x 5 x 14) + (3,14 x 5 x 13)
L = 78,5 +439,6 + 204,1
L = 722,2 cm²
b. Luas Permukaan
Diketahui :
Diameter tabung dan bola = 14 cm
Jari-jari tabung dan bola = 7 cm
Tinggi tabung = 20 cm
Ditanyakan : luas gabungan bangun ruang
Jawab :
Luas gabungan = Luas selimut tabung + luas permukaan bola
L = (2 x phi x r x t) + (4 x phi x r x r)
L = (2 x 22/7 x 7 x 20) + (4 x 22/7 x 7 x 7)
L = 880 + 616
L = 1.496 cm²
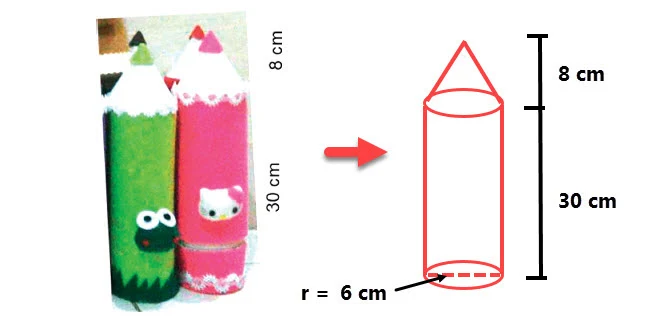
2. Siti membuat kerajinan berbentuk pensil dari kain flannel. Perhatikan Gambar 3.34 berikut.
Jari-jarinya 6 cm. Berapa cm² kain flannel yang digunakan untuk membuatnya?
Diketahui :
Tinggi kerucut = 8 cm
Jari-jari tabung = 6 cm
Tinggi tabung = 30 cm
Ditanyakan : Luas permukaan kerajinan.
Luas selimut kerucut
Hitung panjang garis pelukis (s) kerucut dengan menggunakan cara sebagai berikut :
s² = r² + t²
Keterangan :
s = garis pelukis (cm)
r = jari jari (6 cm)
t = tinggi (8 cm)
Maka cara menghitungnya yaitu :
s² = r² + t²
s² = (6 cm)² + (8 cm)²
s² = 36 cm + 64 cm
s² = 100 cm
s = √100 cm
s = 10 cm
Jawab :
Luas selimut kerucut
Ls= πrs
Ls= 3,14 x 6 x 10
Ls= 3,14 x 60
Ls= 188,4
Luas permukaan tabung tanpa tutup
L =(πr²) + (2πrt)
L =(3,14 x 6 x 6) + (2 x 3,14 x 6 x 30)
L = 113,04 + 1.130,4
L =1. 243,44
Luas gabungan = 188,4 +1.243,44 =1.431,84 cm²
3. Berapakah m² bahan parasit yang dibutuhkan untuk membuat tenda. Perhatikan berikut.
Diketahui :
Panjang balok = 10 cm
Lebar balok = 6 m
Tinggi balok = 1 m
Alas segitiga = 6 m
Tinggi segitiga = 1 m
Ditanyakan : Luas gabungan bangun ruang
Jawab :
Luas balok tanpa alas dan tutup
L = 2 x ( l x t) + (p x l)
L = 2 x (6 x 1) + (10 x 1)
L = 2 x (6+10)
L = 32 m²
Luas prisma segitiga tanpa salah satu sisi
Cari terlebih dahulu sisi miringnya.
s² = r² + t²
s² = (3 m)² + ( 1 m)²
s² = 9 m + 1 m
s² = 10 m
s = √10 m
s = 3,16 m
Luas 2 sisi prisma segitiga
L = 2 x 10 x 3,16
L = 2 x 31,6
L = 63,2 m²
Luas alas dan tutup prisma segitiga
L = 2 x (1/2 x a x t)
L = 2 x (1/2 x 6 x 1)
L = 2 x 3
L = 6 m²
Jadi luas gabungan adalah
L = 32 + 63,2 + 6
L = 101,2 m²
4. Hitunglah luas permukaan bangun tabung tanpa tutup berikut!
Diameternya 14 cm dan tingginya 15 cm.
Diketahui :
Diameter tabung = 14 cm
Tinggi tabung = 15 cm
Ditanyakan : Luas permukaan tabung tanpa tutup
Jawab :
Luas permukaan = luas lingkaran ditambah selimut tabung
L = (πr²) + (2πrt)
L = (22/7 x 7 x 7) + (2 x 22/7 x 7 x 15)
L = 154 + 660
L = 814 cm²
Mohon koreksinya jika ada yang keliru, silahkan tulis di kolom komentar....













Sudah betul
ReplyDeleteHai
ReplyDelete