Berikut ini merupakan tabel rumus luas permukaan beberapa bangun ruang.
| No. | Bangun Ruang | Luas Permukaan |
|---|---|---|
| 1. | Prisma | (2 × La) + (K x t) |
| 2. | Tabung | 2πr(r+t) |
| 3. | Limas | La + Ls |
| 4. | Kerucut | πr (s + r) |
| 5. | Bola | 4πr² |
| 6. | Kubus | 6s² |
| 7. | Balok | 2 ( pl + pt + lt ) |
1. Luas Permukaan Prisma
Sama seperti kubus dan balok, asal usul menentukan luas permukaan prisma dapat dihitung menggunakan jaring-jaring prisma tersebut. Caranya adalah dengan menjumlahkan semua luas bangun datar pada jaring-jaring prisma.
Jika bangun ruang prisma tidak mempunyai bidang alas dan tutup, maka untuk mencari luas permukaannya adalah menjumlahkan luas bidang tegaknya saja.
Ayo Mencoba
1. Diketahui sebuah prisma segitiga dengan alas segitiga siku-siku. Kedua sisi penyikunya 3 cm dan 4 cm. Tinggi prisma 15 cm. Tentukan luas permukaan prisma!
Diketahui:
Prisma dengan alas segitiga siku-siku,
Panjang sisi siku-sikunya 3 cm dan 4 cm.
Tinggi prisma = 15 cm
Ditanya: Luas permukaan prisma
Jawab:
Cari panjang sisi miring pada bidang alas terlebih dahulu.
Sisi miring = √3² + 4²
= √25
= 5 cm
Luas permukaan prisma = 2 x luas alas + keliling alas x tinggi
L = (2 × La) + (K x t)
| L = 2 x ( | 1 | x 3 x 4) + ((3+4+5) x 15) |
| 2 |
L = 12 + 180
L = 192 cm²
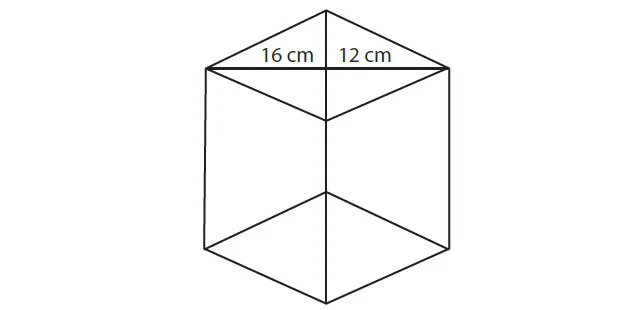
2. Perhatikan Gambar berikut.
Sebuah prisma alasnya berbentuk belah ketupat. Panjang diagonal 16 cm dan 12 cm. Tentukan tinggi prisma jika luas permukaan prisma 512 cm².
Diketahui :
d1 = 16 cm
d2 = 12 cm
Luas = 512 cm²
Ditanyakan : tinggi prisma
Jawab :
Sisi miring = √8² + 6²
= √100
= 10 cm
L = 2 (luas alas) + (keliling alas x t)
L = (2 × La) + (K x t)
| 512 = 2 x ( | 16 x 12 | ) + (4 x 10 x t) |
| 2 |
512 = 192 + 40 t
40t = 512 - 192
40t = 320
t = 320 : 40
t = 8
Maka tinggi prisma adalah 8 cm
4. Tentukan luas permukaan prisma berikut ini!
Diketahui
Prima trapesium sama kaki dengan ukuran:
Tinggi prisma (tp) = 8 cm
Tinggi trapesium (t) = 4 cm
Dua sisi yang sejajar pada trapesium yaitu a = 12 cm dan b = 6 cm
Ditanyakan: Luas permukaan prima = …. ?
Jawab
Sebelum mencari luas permukaan prisma, kita cari dulu panjang sisi miring (m) pada trapesium yaitu diperoleh dengan Pythagoras
m = √(t² + (½ (a – b))²)
m = √(4² + (½ (12 – 6))²)
m = √(16 + (½ (6))²)
m = √(16 + (3)²)
m = √(16 + 9)
m = √(25)
m = 5
Luas alas
L = luas trapesium
L = ½ × jumlah sisi yang sejajar × tinggi
L = ½ × (a + b) × t
L = ½ × (12 cm + 6 cm) × 4 cm
L = ½ × 18 cm × 4 cm
L = 36 cm²
Keliling alas
K = keliling trapesium
K = a + b + m + m
K = 12 cm + 6 cm + 5 cm + 5 cm
K = 28 cm
Jadi luas permukaan prisma trapesium tersebut adalah
L = 2 × luas alas + keliling alas × tinggi
L = (2 × La) + (K x t)
L = 2 × 36 cm² + 28 cm × 8 cm
L = 72 cm² + 224 cm²
L = 296 cm²
5. Sebuah prisma alasnya berbentuk persegi panjang. Luas alas prisma 28 cm². Lebar persegi panjang 4 cm dan tinggi prisma 15 cm. Hitunglah luas permukaan prisma!
Diketahui :
Prisma dengan alas persegi panjang
Luas alas = 28 cm²
Lebar alas = 4 cm
Tinggi prisma = 15 cm
Ditanya :
Luas permukaan prisma =...
Jawab :
Langkah pertama kita cari panjang alas terlebih dahulu
Panjang alas = Luas alas : Lebar alas
P = 28 cm² : 4 cm
P = 7 cm
Langkah kedua kita cari keliling alas prisma
Keliling alas prisma = Keliling persegi panjang
K = 2 x (p + l)
K = 2 x (7 cm + 4 cm)
K = 2 x 11 cm
K = 22 cm
Langkah terahir kita cari luas permukaan prisma
Luas permukaan prisma = (2 x Luas alas) + (Keliling alas x tinggi prisma)
L = (2 × La) + (K x t)
L = (2 x 28) + (22 x 15)
L = 56 + 330
L = 386 cm²
2. Luas Permukaan Tabung
Tabung memiliki 3 sisi berupa dua lingkaran yang disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung. Luas permukaan tabung tanpa tutup adalah menjumlahkan luas alas berupa lingkaran dengan luas selimut.
Ayo Mencoba
Ayo Mencoba
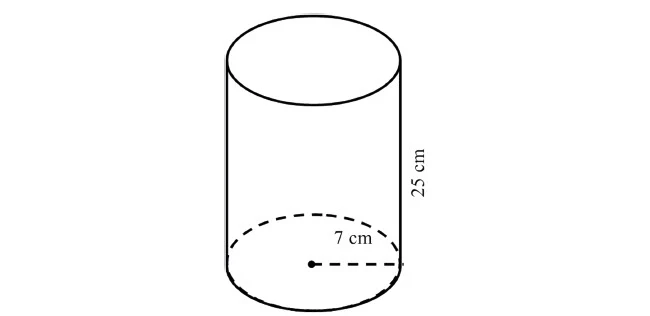
1. Tentukan luas permukaan gambar di berikut
Diketahui :
Tinggi Tabung = 25 cm
Jari - jari = 7 cm
Ditanyakan : Luas Permukaan Tabung
Jawab :
L = 2πr(r+t)
| L = 2 x | 22 | x 7 (7 + 25) |
| 7 |
| L = | 44 | x 7 (32) |
| 7 |
L = 1.408 cm²
2. Diketahui sebuah kaleng cat berbentuk tabung. Diameternya 14 cm dan tingginya 20 cm. Tentukan
luas permukaan kaleng tersebut!
Diketahui:
Diameter tabung = 14 cm
Jari-jari tabung = 7 cm
Tinggi tabung = 20 cm
Ditanya:
Luas permukaan tabung = ... ?
Jawab:
L = 2πr(r + t)
| L = 2 x | 22 | x 7 x (7 + 20) |
| 7 |
L = 44 x 27
L = 1.188 cm²
3. Sebuah tabung dengan panjang jari-jari 10 cm. Luas permukaan tabung adalah 1.570 cm². Berapakah tinggi tabung tersebut?
Diketahui:
r = 10 cm
Luas permukaan tabung = 1570 cm²
Ditanya:
Tinggi tabung (t)=....?
Jawab:
L.permukaan tabung = 2 x π x r x ( t + r)
1570 = 2 x 3,14 x 10 x (t + 10)
1570 = 62,8 x(t + 10)
1570 = 62,8t + 628
62,8t = 1570 - 628
62,8t = 942
t = 942 : 62,8
t = 15 cm
Jadi tinggi tabung tersebut adalah 15 cm
4. Beni akan menghias sebuah gelas berbentuk tabung tanpa tutup. Ukuran diameternya 8 cm dan tingginya 9 cm. Berapakah kain yang dibutuhkan Beni untuk melapisi gelas tersebut?
Diketahui
Sebuah gelas berbentuk tabung tanpa tutup
Diameter (d) = 8 cm
Jari-jari (r) = 4 cm
Tinggi = 9 cm
Ditanya
kain yang dibutuhkan Beni untuk melapisi gelas tersebut adalah ...
Jawab
Luas permukaan tabung tanpa tutup = π x r x (r + 2t)
Luas permukaan tabung tanpa tutup = 3,14 x 4 x (4 + 2. 9)
Luas permukaan tabung tanpa tutup = 3,14 x 4 x 22
Luas permukaan tabung tanpa tutup = 276, 32 cm²
Jadi kain kain yang dibutuhkan Beni untuk melapisi gelas tersebut adalah 276, 32 cm²
5. Hitunglah luas bangun ruang di bawah ini!
Diketahui:
Diameter lingkaran kecil (a ) = 7 cm
Jari jari a = 3,5 cm
Diameter Lingkaran besar (b) =7+2+2=11cm
Jari jari b=5,5
Tinggi = 3 cm
Ditanyakan :
Luas permukaan ?
Jawab:
Luas tutup lingkaran = Luas lingkaran besar - Luas lingkaran kecil
= πrb² - πra²
= (3,14 x 5,5 x 5,5 ) - (22/7 x 3,5 x 3,5)
= (3,14 x 30,25) - (22 x 0,5 x 3,5)
= 94,985 + 38,5
= 56,485
Luas selimut ra
= 2 x πra x t
= 2 x 22/7 x 3,5 x 3
= 2 x 22 x 0,5 x 3
= 66 cm²
Luas Selimut b
= 2 x πrb x t
= 2 x 3,14 x 5,5 x 3
= 103,62 cm²
Luas permukaan selruhnya
=56,485cm² +56,485 cm² +66 cm²+ 103,62 cm²
=282,59 cm²
3. Luas Permukaan Limas
Limas segi-n merupakan bangun ruang yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Tinggi sisi tegak pada limas (berupa segitiga) pada limas dapat ditentukan dengan menggunakan dalil pythagoras.
Ayo Mencoba
1. Tentukan luas permukaan gambar berikut!
a. Limas dengan alas berbentuk belah ketupat
Untuk mengetahui panjang sisi alas kita bisa menggunakan pythagoras.
QR² = 8² + 6²
QR² = 64 + 36
QR² = 100
QR = √100
QR = 10
Jadi panjang sisi alas belah ketupat adalah 10 cm
Luas alas PQRS
L = ¹/₂ × PR × SQ
L = ¹/₂ × 16 × 12 cm²
L = 8 × 12 cm²
L = 96 cm²
Luas segitiga (sisi tegak limas)
L Δ = ¹/₂ × QR × TB
L Δ = ¹/₂ × 10 × 10 cm²
L Δ = 50 cm²
Luas permukaan Limas T.PQRS
L = luas alas + 4 × luas segitiga
L = 96 cm² + (4 × 50 cm²)
L = 96 cm² + 200 cm²
L = 296 cm²
Jadi luas permukaan limas T.PQRS dengan alas berbentuk belah ketupat adalah 296 cm²
b. Limas dengan alas berbentuk segitiga.
Kita bisa gunakan pythagoras untuk mencari tinggi segitiga
tΔ² = 8² - 4²
tΔ² = 64 - 16
tΔ² = 48
tΔ = √48
tΔ = 4√3 cm
tΔ = 6,93 cm
Luas segitiga sama sisi
L Δ = ¹/₂ × s × tΔ
L Δ = ¹/₂ × 8 × 6,93 cm²
L Δ = 4 × 6,93 cm²
L Δ = 27,72 cm²
Luas permukaan limas segitiga sama sisi
L = 4 × L Δ
L = 4 × 27,72 cm²
L = 110,88 cm²
Jadi luas permukaan limas dengan alas berbentuk segitiga sama sisi adalah 110,88 cm²
2. Ibu Beni suka membuat kue koci berbentuk limas. Bentuk alas limas adalah persegi. Panjang sisi
alas 8 cm, dan tinggi sisi tegak 7 cm. Kue tersebut dibungkus daun pisang. Berapa cm² luas daun
pisang yang dibutuhkan untuk membungkus tiga kue koci?
Diketahui :
Panjang alas (s) = 8 cm
Tinggi sisi tegak = 7 cm
Banyak limas kue = 3 buah
Ditanya :
Luas daun pisang yang dibutuhkan untuk membungkus 3 kue koci ?
Jawab :
Luas permukaan limas segiempat beraturan
L = La+ Ls
L = s² + (4 × ¹/₂ × s × t)
L = (8 × 8) cm² + (4 × ¹/₂ × 8 × 7) cm²
L = 64 cm² + 112 cm²
L = 176 cm²
Luas daun pisang untuk membungkus 3 kue koci
L seluruh = banyak kue × luas permukaan limas
L = 3 × 176 cm²
L = 528 cm²
Jadi luas daun pisang yang dibutuhkan untuk membungkus 3 kue koci adalah 528 cm²
3. Ayah Siti akan membangun sebuah gazebo. Atapnya terbuat dari kirai berbentuk limas segiempat beraturan. Sisi pada atap tersebut 2 m. Tinggi sisi tegaknya 2,5 m. Berapa m² luas permukaan atap yang akan dipasang?
Diketahui :
Panjang sisi alas = s = 2 m
Tinggi sisi tegak = t = 2,5 m
Ditanya: berapa luas permukaan atap yang akan di pasang?
Jawab:
Gazebo memiliki atap berbentuk limas segi empat beraturan. Atap berarti limas bagian bawah terbuka sehingga luas permukaan atap = luas keempat sisi tegak limas.
L = 4 x luas sisi tegak limas
L = 4 x 1/2 x alas x tinggi
L = 4 x 1/2 x s x t
L = 4 x 1/2 x 2 m x 2,5 m
L = 2 x 2 m x 2,5 m
L = 10 m²
Jadi luas permukaan atap yang akan dipasang oleh ayah Siti pada gazebo adalah 10 m².
4. Luas Permukaan Kerucut
Luas permukaan kerucut adalah menjumlahkan luas alas berbentuk lingkaran dan luas selimut. Bentuk luas selimut kerucut adalah bidang juring (sektor) lingkaran dengan busur sama dengan keliling lingkaran alas yaitu 2πr.
Ayo Mencoba
Kerjakan soal-soal berikut ini dengan teliti!
1. Tentukan luas permukaan gambar berikut!
Diketahui :
Jari-Jari = 5m
Menentukan garis pelukis
s² = r² + t²
s² = 5² + 12²
s² = 25 + 144
s² = 169
s = √169
s = 13 cm
Luas permukaan kerucut
L = π r (s + r)
L = 3,14 x 5 (13 + 5)
L = 3,14 x 5 x 18
L = 282,6 cm²
2. Sebuah kerucut mempunyai luas permukaan 785 cm² . Jarij-arinya 10 cm. Berapa cm garis pelukis kerucut tersebut?
Diketahui :
Luas = 785 cm²
Jari-jari = 10cm
Ditanyakan : Luas permukaan
Luas permukaan kerucut = πr(r + s)
785 cm² = 3,14 × 10 cm (10 cm + s)
785 = 31,4 (10 + s)
10 + s = 785 ÷ 31,4
10 + s = 25
s = 25 - 10
s = garis pelukis kerucut = 15 cm.
3. Diameter kerucut 28 cm. Garis pelukisnya 20 cm. Hitung luas permukaannya dalam cm²!
Diketahui :
Diameter kerucut = 28 cm
Jari-jari (r) = 28 : 2 = 14 cm
garis pelukis (s) = 20 cm
Ditanya :
Luas permukaan kerucut ?
Jawab :
Menghitung luas permukaan kerucut
L = π r (r + s)
L = 22/7 × 14 (14 + 20) cm²
L = 22 × 2 × 34 cm²
L = 1.496 cm²
4. Wayan akan membuat topi ulang tahun berbentuk kerucut. Keliling lingkaran alas 56,52 cm dan garis pelukisnya 20 cm. Berapa cm² luas kertas yang dibutuhkan untuk membuat topi?
Diketahui :
K = 56,52 cm
s = 20 cm
Ditanyakan : Luas kertas
Keliling = 2π r
56,52 = 2π r
r = 56,52 / 6,28
r = 9 cm
s = 20 cm
L = πrs
L = 3,14 x 9 x 20
L = 565,2 cm²
Jadi luas kertas yang dibutuhkan untuk membuat topi adalah 565,2 cm²
5. Luas Permukaan Bola
Luas permukaan bola sama dengan empat kali luas lingkaran dengan panjang jari-jari yang sama.
Ayo Mencoba
Kerjakan soal berikut dengan cermat!
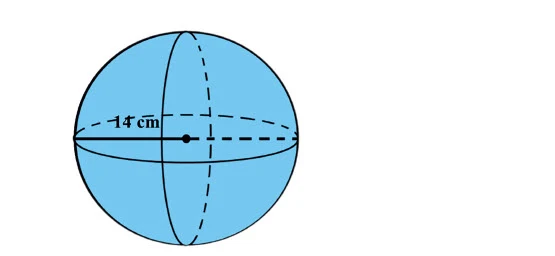
1. Tentukan luas permukaan gambar berikut!
Diketahui :
Jari-jari = 14 cm
Ditanyakan : Luas permukaan
Jawab :
L =4πr²
| L = 4 x | 22 | x 14 x 14 |
| 7 |
L = 2.464 cm²
2. Diameter sebuah bola 24 cm. Bola tersebut terbuat dari kulit sintetis. Berapa cm² luas kulit sintetis yang dibutuhkan?
Diketahui:
Diameter (d) = 24 cm
Jari jari (r) = 1/2 × 24 = 12 cm
Ditanyakan:
Luas kulit sintetis yang dibutuhkan = ... ?
L =4πr²
L =4×3,14×12×12
L =12,56×144
L =1.804,64 cm²
3. Diketahui sebuah bola dengan luas permukaan 314 cm². Hitunglah jari-jari bola tersebut!
Diketahui:
L = 314 cm²
Ditanyakan:
Jari jari (r) bola = ... ?
Penyelesaian:
L =4πr²
314 = 4 x 3,14 x r²
314 = 12,56 x r²
| r² = | 314 | |
| 12,56 |
r =√25
r = 5
4. Kubah masjid Wali Songo berbentuk setengah bola.. Diameter kubah masjid 3,5 m. Berapa m² luas kubah masjid tersebut?
Diketahui :
Diameter kubah = 3,5 m
Jari-jari kubah = 1,75 m
Ditanyakan : Luas kubah
Jawab :
| L = | 1 | x 4πr² |
| 2 |
| L = 2 x | 22 | x 1,75 x 1,75 |
| 7 |
| L = | 44 | x 1,75 x 1,75 |
| 7 |
5. Sebuah kayu padat berbentuk setengah bola. Kayu tersebut akan dibungkus dengan kain. Jari-jari kayu 3 cm. Berapa cm² luas kain yang dibutuhkan?
Diketahui :
Jari-jari : 3 cm
Ditanyakan : Luas kain yang dibutuhkan.
| L = | 1 | x 4πr² |
| 2 |
| L = | 1 | x 4 x 3 x 3 |
| 2 |
L = 6,28 × 9 cm²
L = 56,52 cm²













Bagussoalnya
ReplyDelete