A. Menentukan KPK Dua Bilangan atau Lebih
KPK atau Kelipatan Persekutuan Terkecil adalah bilangan bulat positif dengan nilai terkecil yang bisa habis bila dibagi dengan kedua bilangan tersebut Untuk menentukan KPK dua buah bilangan dapat dilakukan dengan menggunakan faktorisasi prima dan kelipatan bilangan. Perhatikan beberapa contoh berikut ini
1. Menggunakan Kelipatan Kedua Bilangan
Kelipatan bilangan adalah bilangan-bilangan yang merupakan hasil kali bilangan tersebut dengan bilangan bulat positif. Kelipatan bilangan dapat digunakan untuk menentukan KPK dua bilangan atau lebih. Perhatikan contoh soal berikut ini !
Berapakah KPK dari 4 dan 6?
Penyelesaian
Kelipatan 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 40, …Kelipatan 6 adalah 6, 12, 18, 24, 30, 36, …Kelipatan persekutuan dari 4 dan 6 adalah 12, 24, …Jadi, KPK dari 4 dan 6 adalah 12.
2. Menggunakan Pohon Faktor
Pohon faktor merupakan deretan pembagian yang turun kebawah dengan menggunakan pembagian menggunakan bilangan prima. Cara menentukan KPK dua bilangan atau lebih dapat dilakukan dengan langkah-langkah sebagai berikut :
- Tulislah bilangan-bilangan tersebut dalam bentuk perkalian faktor prima.
- Ambil semua faktor yang sama dari bilangan-bilangan tersebut.
- Apabila faktor yang sama tersebut memiliki pangkat yang berbeda, maka ambil faktor yang pangkatnya terbesar.
Berapakah KPK dari 4 dan 6?
Penyelesaian
Faktorisasi prima dari 4 = 2²Faktorisasi prima dari 6 = 2 × 3Jadi KPK 4 dan 6 adalah = 2² x 3 = 4 x 3 = 12
B. Menentukan FPB Dua Bilangan atau Lebih
1. Menggunakan Faktor Persekutuam
Faktor persekutuan merupakan bilangan faktor yang sama dari dua bilangan atau lebih. FPB diambil dari faktor yang memiliki nilai terbesar.. Perhatkan contoh soal berikut ini!
Carilah FPB dari 6, 9, dan 18 ...
Pembahasan
Faktor dari 6 adalah = {1, 2, 3, 6}
Faktor dari 9 adalah = {1, 2, 3, 9}
Faktor dari 18 adalah = {1, 2, 3, 6, 9, 18}
Faktor persekutuan dari ketiga bilangan tersebut adalah 1, 2, 3
Nilai terbesar dari faktor tersebut adalah 3 maka FPB dari 6, 9, dan 18 adalah 3
2. Menggunakan Pohon Faktor
Pohon faktor merupakan deretan pembagian yang turun kebawah dengan menggunakan pembagian menggunakan bilangan prima. Cara menentukan FPB menggunakan phon faktor adalah sebagai berikut !
- Tulislah bilangan-bilangan tersebut ke dalam bentuk perkalian faktor prima.
- Setelah itu ambillah faktor yang sama dari bilangan-bilangan tersebut.
- Apabila faktor yang sama tersebut memiliki pangkat yang berbeda, maka ambillah faktor yang memiliki nilai pangkat terkecil.
Perhatikan contoh soal berikut ini !
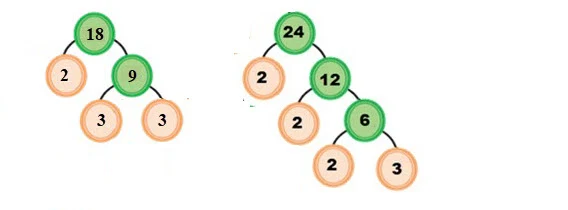
Tentukan FPB dari 18 dan 24
Pembahasan :
Faktor 18 = 2 x 3 x 3 = 2 x 3²Faktor 24 = 2 x 2 x 2 x 3 = 2³ x 3FPB = 2 x 3 = 6Jadi FPB dari 18 dan 24 adalah 6
Ayo Mencoba
1. Tentukan pohon faktor setiap pasangan bilangan berikut.
a. 6 dan 9
b. 9 dan 12
c. 20 dan 30
d. 32 dan 48
e. 12 dan 18
2. Tentukan KPK dua bilangan berikut dengan menggunakan faktorisasi prima.
a. 10 dan 12
Faktorisasi prima dari 10 = 2 × 5Faktorisasi prima dari 12 = 2² × 3Maka KPKnya = 2² x 3 x 5 = 4 x 3 x 5 = 60
b. 15 dan 20
Faktorisasi prima dari 15 = 3 × 5Faktorisasi prima dari 20 = 2² x 5Maka KPKnya = 2² × 3 × 5 = 4 × 3 × 5 = 60
e. 18 dan 20
Faktorisasi prima dari 18 = 2 x 3²Faktorisasi prima dari 20 = 2² x 5Maka KPKnya = 2² x 3² x 5 = 4 × 9 × 5 = 180
d. 42 dan 54
Faktorisasi prima dari 42 = 2 x 3 × 7Faktorisasi prima dari 54 = 2 x 3³Maka KPKnya = 2 x 3³ x 7 = 2 × 27 × 7 = 378
e. 38 dan 40
Faktorisasi prima dari 38 = 2 x 19Faktorisasi prima dari 40 = 2³ × 5Maka KPKnya = 2³ × 5 × 19 = 8 × 5 × 19 = 760
3. Tentukan KPK tiga bilangan berikut dengan menggunakan faktorisasi prima.
a. 6, 8 dan 9
Faktorisasi prima :6 = 2 × 38 = 2³9 = 3²KPK = 2³ × 3² = 8 × 9 = 72Jadi KPK dari bilangan 6, 8 , dan 9 adalah 72.
b. 9, 10 dan 12
Faktorisasi prima :9 = 3²10 = 2 × 512 = 2² × 3KPK = 2² × 3² × 5 = 4 × 9 × 5 = 180Jadi KPK dari bilangan 9, 10, dan 12 adalah 180.
c. 12, 16 dan 18
Faktorisasi prima :12 = 2² × 316 = 2⁴18 = 2 × 3²KPK = 2⁴ × 3² = 16 × 9 = 144Jadi KPK dari bilangan 12, 16, dan 18 adalah 144.
d. 15, 20 dan 30
Faktorisasi prima :15 = 3 × 520 = 2² × 518 = 2 × 3 × 5KPK = 2² × 3 × 5 = 4 × 3 × 5 = 60Jadi KPK dari bilangan 15, 20, dan 30 adalah 60.
e. 32, 36 dan 48
Faktorisasi prima :32 = 2⁵36 = 2² × 3²48 = 2⁴ × 3KPK = 2⁵ × 3² = 32 × 9 = 288Jadi KPK dari bilangan 32, 36, dan 48 adalah 288.
A. Menentukan FPB Dua Bilangan
Faktor persekutuan adalah faktor yang sama dari dua bilangan atau lebih.
Ayo Mencoba
1. Tentukan FPB dua bilangan berikut dengan menggunakan faktor persekutuan.
a. 6 dan 9
Faktor 6 = 1, 2, 3, 6Faktor 9 = 1, 3, 9Faktor persekutuan dari 6 dan 9 = 1 , dan 3FPB dari 6 dan 9 = 3
b. 9 dan 12
Faktor 9 = 1, 3, 9Faktor 12 = 1, 2, 3, 4, 6, 12Faktor persekutuan dari 9 dan 12 = 1 , dan 3FPB dari 9 dan 12 = 3
c. 12 dan 18
Faktor 12 = 1, 2, 3, 4, 6, 12Faktor 18 = 1, 2, 3, 6, 9, 18Faktor persekutuan dari 12 dan 18 = 1, 2 , 3, dan 6FPB dari 12 dan 18 = 6
d. 20 dan 30
Faktor 20 = 1, 2, 4, 5, 10, 20Faktor 30 = 1, 2, 3, 5, 6, 10, 15, 30Faktor persekutuan dari 20 dan 30 = 1, 2, 5, dan 10FPB dari 20 dan 30 = 10
e. 32 dan 48
Faktor 32 = 1, 2, 4, 8, 16, 32Faktor 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48Faktor persekutuan dari 32 dan 48 = 1, 2, 4 , 8, dan 16FPB dari 32 dan 48 = 16
2. Tentukan FPB dua bilangan berikut dengan menggunakan faktorisasi prima.
a. 10 dan 12
Faktorisasi 10 = 2 × 5Faktorisasi 12 = 2² × 3FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.Jadi FPB dari 10 dan 12 adalah 2
b. 15 dan 20
Faktorisasi 5 = 3 × 5Faktorisasi 20 = 2² × 5FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.Jadi FPB 15 dan 20 adalah 5
c. 18 dan 20
Faktorisasi 18 = 2 × 3²Faktorisasi 20 = 2² × 5FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.Jadi FPB 18 dan 20 adalah = 2
d. 38 dan 40
Faktorisasi 38 = 2 × 19Faktorisasi 40 = 2³ × 5FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.Jadi FPB dari 38 dan 40 adalah = 2
e. 42 dan 54
Faktorisasi 42 = 2 × 3 × 7Faktorisasi 54 = 2 × 3³FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.Jadi FPB dari 42 dan 54 adalah = 2 × 3 = 6
3. Tentukan FPB tiga bilangan berikut dengan menggunakan faktor persekutuan.
a. 6, 8 dan 9
Faktor 6 = 1, 2, 3, 6Faktor 8 = 1, 2, 4, 8Faktor 9 = 1, 3, 9Faktor persekutuan dari 6, 8 dan 9 = 1FPB dari 6, 8 dan 9 = 1
b. 9, 10 dan 12
Faktor 9 = 1, 3, 9Faktor 10 = 1, 2, 5, 10Faktor 12 = 1, 2, 3, 4, 6, 12Faktor persekutuan dari 9, 10 dan 12 = 1FPB dari 9, 10 dan 12 = 1
c. 12, 16 dan 18
Faktor 12 = 1, 2, 3, 4, 6, 12Faktor 16 = 1, 2, 4, 8, 16Faktor 18 = 1, 2, 3, 6, 9, 18Faktor persekutuan dari 12, 16 dan 18 = 1, 2FPB dari 12, 16 dan 18 = 2
d. 15, 20 dan 30
Faktor 15 = 1, 3, 5, 15Faktor 20 = 1, 2, 4, 5, 10, 20Faktor 30 = 1, 2, 3, 5, 6, 10, 15, 30Faktor persekutuan dari 15, 20 dan 30 = 1, 5FPB dari 15, 20 dan 30 = 5
e. 32, 36 dan 48
Faktor 32 = 1, 2, 4, 8, 16, 32Faktor 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36Faktor 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48Faktor persekutuan dari 32, 36 dan 48 = 1, 2, 4FPB dari 32, 36 dan 48 = 4











0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.