Bilangan merupakan suatu konsep dalam matematika yang digunakan untuk melakukan pencacahan dan pengukuran. Secara sederhana dapat disebutkan bahwa bilangan digunakan untuk menyatakan banyak atau jumlah suatu objek. Bilangan bulat adalah bilangan yang terdiri atas bilangan bulat positif, bilangan nol dan bilangan bulat negatif. Operasi hitung bilangan bulat ada 4 macam yaitu operasi hitung penjumlahan, pengurangan, perkalian, dan pembagian.
A. Penjumlahan Bilangan Bulat
Dalam menghitung hasil penjumlahan dua bilangan bulat, dapat digunakan dengan menggunakan garis bilangan. Bilangan yang dijumlahkan digambarkan dengan anak panah dengan arah sesuai dengan bilangan tersebut. Apabila bilangan positif, anak panah menunjuk ke arah kanan.Sebaliknya, apabila bilangan negatif, anak panah menunjuk ke arah kiri.
Seseorang berdiri di atas lantai berpetak. Ia memilih satu garis lurus yang menghubungkan petak-petak lantai tersebut. Ia berdiri di satu titik dan ia namakan titik 0. Penjumlahan pada garis bilangan:dilakukan dengan aturan sebagai berikut.
- Operasi penjumlahan, berarti menghadap pada arah yang tetap.
- Tanda positif, berarti maju.
- Tanda negatif, berarti mundur.
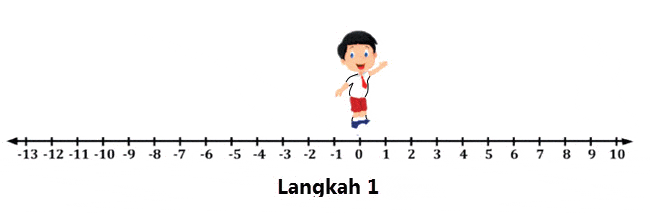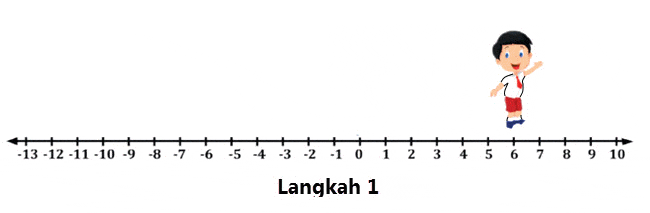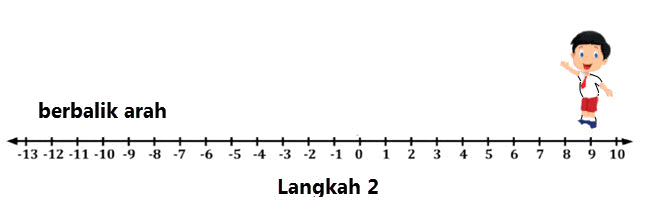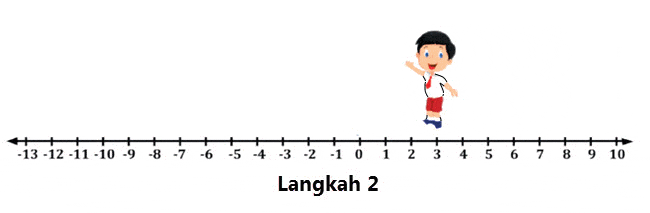
Perhatikan langkah-langkah penjumlahan berikut!
Langkah 1
Bilangan 9 atau positif 9, artinya maju 9 langkah ke depan dari 0
Langkah 2
Penjumlahan, artinya menghadap pada arah yang tetap.
Langkah 3
Bilangan –6 atau negatif 6 artinya mundur 6 langkah ke belakang dari 9.
Jadi, hasil dari 9 + (–6) adalah 3
Coba hitung soal berikut!
(–8) + 4 = ...
Penyelesaian
Perhatikan langkah-langkah berikut!
Langkah 1
Bilangan –8 atau negatif 8, artinya bilangan tersebut mundur 8 langkah ke belakang dari 0.
Langkah 2
Penjumlahan, artinya menghadap pada arah yang tetap.
Langkah 3
Bilangan 4 atau positif 4, artinya bilangan tersebut maju 4
Jadi, hasil dari (–8) + 4 adalah –4
Sifat-Sifat Penjumlahan Bilangan Bulat
Sifat-sifat pada penjumlahan bilangan bulat ada dua (2), yaitu komutatif dan assosiatif.
a. Sifat komutatif
Sifat komutatif adalah sifat pertukaran dua bilangan pada operasi hitung penjumlahan, dimana pengerjaan operasi hitung dua bilangan yang ditukarkan tempatnya tersebut hasilnya sama. Sifat komutatif disebut juga sifat pertukaran. Hal ini dapat dituliskan sebagai berikut. Untuk setiap bilangan bulat a dan b, selalu berlaku a + b = b + a.
Apakah 3 + 4 = 4 + 3? Jika ya, maka penjumlahan bilangan bulat tersebut mempunyai sifat komutatif. Jika tidak, maka bilangan bulat tersebut tidak bersifat komutatif. Penjumlahan bilangan bulat bersifat asosiatif.
b. Sifat asosiatif
Sifat assosiatif dalam penjumlahan adalah mengelompokkan tiga bilangan atau lebih dengan urutan berbeda. Sifat komutatif disebut juga sifat pertukaran. Penjumlahan dua bilangan bulat selalu diperoleh hasil yang sama walaupun kedua bilangan tersebut dipertukarkan tempatnya. Hal ini dapat dituliskan sebagai berikut. Untuk setiap bilangan bulat a dan b, selalu berlaku
a + b = b + a.
Apakah 3 + (4 + 5) = (3 + 4) +5? Jika ya, maka penjumlahan bilangan bulat tersebut mempunyai sifat assosiatif. Jika tidak, maka bilangan bulat tersebut tidak bersifat assosiatif. Penjumlahan pada bilangan bulat bersifat asosiatif.
Contoh
1. Apakah 7 + 13 = 13 + 7?
Penyelesaian
Penjumlahan bersifat komutatif, sehingga 7 + 13 = 13 + 7.
2. Isilah titik-titik berikut!
6 + (... + 14) = (6 + 12) + ...
Penyelesaian
Penjumlahan bersifat assosiatif, sehingga
6 + (12 + 14) = (6 + 12) + 14
B. Pengurangan Bilangan Bulat
Seperti pada penjumlahan bilangan bulat, untuk menghitung hasil pengurangan dua bilangan bulat dapat digunakan bantuan garis bilangan. Pengurangan pada garis bilangan:dilakukan dengan aturan sebagai berikut.
- Operasi pengurangan, berarti berbalik arah.
- Tanda positif, berarti maju.
- Tanda negatif, berarti mundur.
Perhatikan langkah-langkah penjumlahan berikut!
Coba hitung soal berikut!
9 – 6 = ...
Penyelesaian
Perhatikan langkah-langkah berikut!
Langkah 1
Bilangan 9 atau positif 9, artinya bilangan tersebut maju 9 langkah ke depan dari 0.
Langkah 2
Pengurangan, artinya berbalik arah.
Langkah 3
Bilangan 6 atau positif 6, artinya maju 6 langkah ke depan dari 9.
Jadi, hasil dari 9 – 6 adalah 3.
Kerjakan soal berikut!
4 – (–5) = ...
Penyelesaian
Perhatikan langkah-langkah berikut!
Langkah 1
Bilangan 4 atau positif 4, artinya maju 4 langkah ke depan dari 0.
Langkah 2
Pengurangan, artinya berbalik arah dari langkah 1
Langkah 3
–5 atau negatif 5, artinya mundur 5 langkah ke belakang.
Jadi, hasil dari 4 – (–5) adalah 9.
Sifat-Sifat Pengurangan Bilangan Bulat
Sifat-sifat operasi hitung pengurangan antara lain sebagai berikut
a. Tidak Asosiatif
Apakah 7 – (4 – 2) = (7 – 4) – 2? Jika ya, maka pengurangan bilangan bulat tersebut mempunyai sifat assosiatif. Jika tidak, maka pengurangan bilangan tersebut tidak bersifat assosiatif. Pengurangan pada bilangan bulat bersifat tidak asosiatif.
b. Tidak Komutatif
Apakah 4 – 3 = 3 – 4? Jika ya, maka pengurangan bilangan bulat tersebut mempunyai sifat komutatif. Jika tidak, maka pengurangan bilangan tersebut tidak bersifat komutatif. Pengurangan bilangan bulat tidak komutatif.
Contoh :
1. Apakah 10 – 4 = 4 – 10?
Penyelesaian
Pengurangan tidak bersifat komutatif, sehingga
10 – 4 ≠ 4 – 10
2. Apakah 6 – (2 – 1) = (6 – 2) – 1?
Penyelesaian
Pengurangan tidak bersifat assosiatif, sehingga
6 – (2 – 1) ≠ (6 – 2) – 1
Tanda ≠ merupakan tanda ketidaksamaan yang dibaca tidak sama dengan.
Ayo Mencoba
1. Ubahlah kalimat matematika berikut ke dalam garis bilangan!
a. –5 + 12 = 7
b. 10 + (–8 ) = 2
c. 8 – (–7) = 15
d. –11 – (–8) = –3
e. –2 + (–8) – (–7) = –3
2. Ubahlah garis bilangan berikut menjadi kalimat matematika!
Nomor 2a = -5 + (-6) = -11
Nomor 2b = 7 + (-9) = -2
3. Tentukan hasil penjumlahan dan pengurangan bilangan bulat berikut!
a. –12 + 7 = -5
b. 10 – (–14) = 10 + 14 = 24
c. –25 + (–53) = -78
d. 15 + (-35) = –20
e. 27 – (–23) = 50
4. Sebuah bola dilemparkan ke atas hingga ketinggian 5 meter. Bola tersebut jatuh ke dalam sumur di kedalaman 4 meter. Berapa meter jarak yang ditempuh bola dari posisi awal hingga akhir?
5 - (-4) = 5 + 4 = 9
5. Suhu badan seorang anak ketika demam 39°C. Setelah diberikan obat penurun demam, suhu badan turun 4°C. Tentukan suhu badan anak setelah diberikan obat.
39°C - 4°C = 35°C














0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.