Pada pembelajaran Matematika Kelas V Sekolah Dasar Kurikulum Merdeka Bab 3 Perkalian Bilangan Desimal terdapat kegiatan pembahasan tentang Persoalan Perkalian Bilangan Desimal. Tujuan kegiatan pembelajaran kali ini adalah peserta didik dapat memeriksa materi yang sudah dipelajari, memikirkan tentang jumlah tempat desimal sehingga hasil perkaliannya menjadi bilangan bulat, dan memikirkan tentang kalkulasi yang membuat produk menjadi terbesar (terkecil).
Perkalian Bilangan Desimal
Dalam mengerjakan perkalian desimal, hal yang harus diperhatikan adalah jumlah angka yang terletak setelah tanda koma. Cara mengalikannya yaitu dengan menghilangkan terlebih dahulu tanda koma, kemudian mengembalikan tanda koma yang dihilangkan setelah selesai menghitung perkalian.
Ketika mengalikan bilangan desimal dengan bilangan desimal dalam bentuk vertikal, tempatkan tanda koma dari bilangan hasil perkalian dengan menjumlahkan tanda koma dari bilangan pengali dan bilangan yang dikalikan serta dihitung dari kanan.
Pada perkalian dengan bilangan desimal yang kurang dari 1 berlaku aturan sebagai berikut
- Jika bilangan pengali adalah bilangan desimal yang kurang dari 1, maka bilangan hasil perkalian akan lebih kecil dari bilangan yang dikalikan.
- Jika bilangan pengali lebih dari 1 maka bilangan hasil perkalian lebih besar dari bilangan yang dikalikan.
- Jika bilangan pengali kurang dari 1 maka bilangan hasil perkalian lebih kecil dari bilangan yang dikalikan.
Pada penjumlahan bilangan desimal berlaku aturan atau sifat sebagai berikut
- Ketika 2 bilangan dijumlahkan, hasil penjumlahan akan tetap sama meskipun urutan dari 2 bilangan tersebut dibalik.(Komutatif)
- Ketika 3 bilangan dijumlahkan, hasil penjumlahan akan tetap sama meskipun urutan pengerjaannya berubah.(Asosiatif)
Pada perkalian bilangan desimal berlaku aturan/sifat sebagai berikut
- Ketika 2 bilangan dikalikan, hasil perkalian akan tetap sama meskipun urutan dari 2 bilangan tersebut dibalik. (Komutatif).
- Ketika 3 bilangan dikalikan, hasil perkalian akan tetap sama meskipun urutan pengerjaannya berubah.(Asosiatif)
A. Persoalan 1
1. Simpulkan bagaimana cara menghitung dengan bilangan desimal.
Untuk anak-anak yang tidak tahu apa yang harus dimasukkan kotak untuk kotak dikalikan dengan 2,3; minta mereka memperhatikan "3.68 jawaban" dan pikirkan tentang angka yang akan dimasukkan ke dalam kotak dengan mengingatkan mereka bahwa jawabannya bukan 2,3 × 1,6 dan saat mengalikan desimal jawabannya dihitung setelah diubah menjadi bilangan bulat.Untuk menghitung 2,3 × 1,6 pertama-tama kalikan 2,3 dengan dan kalikan 1,6 dengan 10 Lalu hitunglah 23 × 16 dan kalikan jawabannya yaitu 368 dengan 1/100.
2. Ayo hitunglah dalam bentuk vertikal !
3. Ada sebuah pita yang harganya Rp 900,00 per 1 m.
1 Berapakah harga dari 3,2 m pita tersebut?
90 × 3,2 = 288
2 Berapakah harga dari 0,6 m pita tersebut?
90 × 0,6 = 54
Untuk memahami hubungan antara produk dan pengali. Peserta didik akan diingatkan bahwa hasil perkaliannya bisa lebih kecil dari pengali dalam perkalian. Peserta didik mampu memahami berat batangan dan panjang pita dengan menggunakan diagram pita.
4. Seorang siswa membuat kesalahan dengan menambahkan 2,5 ke sebuah bilangan dan mendapatkan jawaban yaitu 12,3. Soal yang sebenarnya adalah mengalikan sebuah bilangan tersebut dengan 2,5. Berapakah jawaban dari soal yang sebenarnya?
x + 2,5 = 12,3x = 12,3 − 2,5= 9,89,8 × 2,5 = 24,5
Untuk memperdalam pemahaman tentang penjumlahan dan perkalian desimal dengan mempertimbangkan kebalikan dari perhitungan tertentu.
5. Ayo hitunglah dengan cara yang paling mudah. Tunjukkanlah bagaimana caramu menghitungnya
Mampu menggunakan hukum asosiatif dan hukum distribusi untuk membuat perhitungan ter-skema.
6. Ayo jelaskan cara perhitungan 3,26 × 1,4 dengan menggunakan perhitungan 326 × 14.
Jelaskan mekanisme penghitungan 3,26 x 1,4 menggunakan aturan penghitungan.
B. Persoalan 2
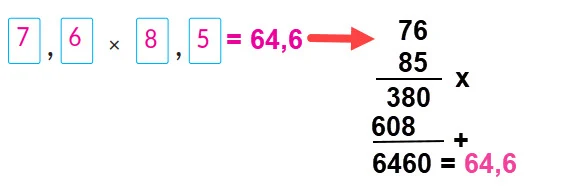
1. Menggunakan 4 kartu dari 6 kartu di bawah ini, buatlah bermacam-macam kalimat matematika dari (bilangan desimal) × (bilangan desimal).
Buat soal dengan memasukkan berbagai angka di kotak dan jawablah menggunakan matematika tertulis.
Apakah bilangan hasil perkaliannya selalu memiliki dua angka di belakang koma?
Tidak
2. Ayo buatlah semua kalimat matematika di mana hasil perkaliannya adalah bilangan bulat. Jelaskanlah bagaimana caramu menghitungnya.
Setelah beberapa soal latihan, minta peserta didik memperhatikan balon bicara yang bertuliskan, "Apakah hasil kali selalu berupa angka sampai dua tingkat desimal?" dan minta mereka melihat fakta bahwa hasil kali satu tempat desimal juga bisa menjadi hasil kali bilangan bulat.
Demikian penjelasan mengenai Persoalan Perkalian Bilangan Desimal. Semoga tulisan ini bermanfaat.
Sumber : Buku Matematika Kelas V Kurikulum Merdeka, Kemendikbud.
0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.