Persoalan Pembagian dengan Bilangan 2 Angka
Untuk melakukan pembagian, tentukan nilai tempat dari hasil baginya, tuliskan bilangan tersebut kemudian kalikan, kurangkan dengan yang dibagi, dan bawa ke bawah hasilnya. Ulangi langkah ini sampai selesai.
Dua prosedur diperlukan agar hasil bagi sementara ini menjadi hasil bagi yang sebenarnya.Yang pertama adalah memastikan bahwa (bilangan pembagi) x (hasil bagi sementara) sama dengan atau lebih kecil dari bilangan yang dapat dibagi dalam operasi "bagi → kali → kurang".Yang kedua adalah memastikan bahwa selisihnya lebih kecil dari angka yang dikurangkan.Ketika keduanya tepat, dapat dikatakan bahwa hasil bagi sementara menjadi hasil bagi yang sebenarnya.
Persoalan 1
1. Ayo, rangkum cara pembagian dengan bilangan 2 angka. (Memahami pembagian dengan bilangan 2 angka secara bersusun)
① Hasil baginya dituliskan mulai dari nilai tempat.
Puluhan
② Hasil bagi pada nilai tempat puluhan, dihitung dari :
76 : 32
③ Perhitungan hasil baginya berada di nilai tempat satuan yaitu
128 : 32
2. Ayo, hitung bersusun. (Melakukan pembagian dengan bilangan dua angka)
① 64 : 21 = 3 sisa 1② 74 : 15 = 4 sisa 14③ 505 : 55 = 9 sisa 10④ 715 : 42 = 17 sisa 1⑤ 567 : 28 = 20 sisa 7⑥ 736 : 36 = 20 sisa 16
4. Jelaskan mengapa perhitungan 320 : 40 dapat dilakukan dengan 32 : 4. (Menjelaskan aturan pembagian)900 : 75 = 12
Ketika kita melakukan pembagian, hasil baginya akan tetap sama jika yang dibagi dan pembaginya dikalikan dengan bilangan yang sama. Hasil baginya akan tetap sama jika yang dibagi dan pembaginya dibagi dengan bilangan yang sama.
5. Ayo, cari bilangan pada tempat yang kosong sehingga hasil kali tiga bilangan pada arah mendatar, tegak, dan diagonal hasilnya sama. (Menggunakan perkalian dan pembagian dalam berbagai cara.)
Persoalan 21.Untuk melakukan pembagian berikut ini, Yosef menggunakan tabel perkalian di atas. Ayo, jelaskan aturan pembagian yang dipakai Yosef.(Gunakan tabel perkalian dan aturan pembagian dalam menghitung.)
72 : 12 = (8×9) : (4×3)
= (2×9) : 3
= (2×3) : 1
= 6
① Ayo, gunakan cara Yosef untuk menghitung soal berikut ini.
64 : 16
64 : 16 = (8 x 8) : (4 x 4) = (8 : 4) x (8 : 4) = 2 x 2 = 4. Jadi 64 : 16 = 4
81 : 27
81 : 27 = (9 x 9) : (3 x 9) = (9 : 3) x (9 : 9) = 3 x 1 = 3. Jadi 81 : 27 = 3
56 : 14
56 : 14 = (8 x 7) : (2 x 7) = (8 : 2) x (7 : 7:) = 4 x 1 = 4. Jadi 56 : 14 = 4
Jauhnya Lompatan
1. Tinggi Heru 135 cm. Dia melompat 270 cm.Berapa kali tinggi badannya jauh lompatannya Heru?
270 : 135 = 2 kali
2. Seorang atlet melompat 8 m 50 cm di suatu lomba lompat jauh. Tingginya 170 cm. Berapa kali tinggi badannya jauh lompatan atlet tersebut?
850 : 170 = 5 kali
3 Seekor katak dapat melompat sejauh 40 kali panjang tubuhnya.
① Panjang tubuh seekor katak 5 cm. Berapa cm katak ini bisa melompat?
5 x 40 = 200. 200 cm = 2 m
② Jika kamu bisa melompat sejauh 40 kali tinggi tubuhmu, berapa jauh lompatanmu dalam m dan cm?
137 x 40 = 5480 . 5480 cm = 54 m 80 cm
Demikian pembahasan mengenai Persoalan Pembagian dengan Bilangan 2 Angka. Semoga tulisan ini bermanfaat.
Sumber : Buku Matematika Kelas IV Kurikulum Merdeka, Kemendikbud.

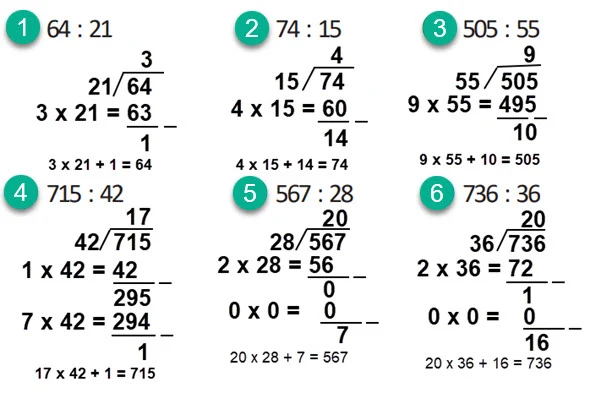














0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.