KD 4.7 Menyelesaikan masalah berkaitan dengan keliling dan luas daerah persegi, persegipanjang, dan segitiga. Salah satu meteri yang dibahas pada KD tersebut adalah pangkat dua dan akar pangkat dua.
Bilangan pangkat dua dicari dengan melakukan perkalian berulang dari bilangan tersebut. Bilangan akar pangkat dua adalah kebalikan pangkat dua adalah akar pangkat dua (√). Berikut ini penjelasan mengenai Bilangan Pangkat Dua dan Akar Pangkat 2 yang dipelajari di kelas 4 sekolah dasar.
A. Pangkat Dua Suatu Bilangan
Contoh 1 :
2. Cara KeduaPangkat dua atau bilangan kuadrat (bahasa Inggris: square) dalam matematika adalah hasil perkalian antara suatu bilangan dengan bilangan itu sendiri atau lebih sederhananya bilangan kuadrat merupakan perkalian berulang.
Pangkat dua suatu bilangan umumnya ditulis dengan a2 = a x a atau mengkuadratkan suatu bilangan sama artinya dengan mengalikan bilangan itu dengan dirinya sendiri. Maka perkalian berulang tersebut dapatditulis dalam bentuk bilangan berpangkat dua. Bentuk perpangkatan yang dimaksud adalah a x a = a2. Perhatikan beberapa contoh berikut ini :
- 4 x 4 dapat ditulis sebagai 4², dibaca 4 pangkat dua.
- 15 x 15 dapat ditulis 15², dibaca 15 pangkat dua.
- 20 x 20 dapat ditulis sebagai 20², dibaca 20 pangkat dua.
Untuk memudahkan menghafal bilangan pangkat dua, berikut ini Daftar Bilangan Pangkat Dua 1 sampai dengan 100 :
| 1 - 10 | 11 - 20 | 21 - 30 | 31 - 40 | 41 - 50 |
|---|---|---|---|---|
| 1² = 1 2² = 4 3² = 9 4² = 16 5² = 25 6² = 36 7² = 49 8² = 64 9² = 81 10² = 100 | 11² = 121 12² = 144 13² = 169 14² = 196 15² = 225 16² = 256 17² = 289 18² = 324 19² = 361 20² = 400 | 21² = 441 22² = 484 23² = 529 24² = 576 25² = 625 26² = 676 27² = 729 28² = 784 29² = 841 30² = 900 | 31² = 961 32² = 1.024 33² = 1.089 34² = 1.156 35² = 1.225 36² = 1.296 37² = 1.369 38² = 1.444 39² = 1.521 40² = 1.600 | 41² = 1.681 42² = 1.764 43² = 1.849 44² = 1.936 45² = 2.025 46² = 2.116 47² = 2.209 48² = 2.304 49² = 2.401 50² = 2.500 |
| 51 - 60 | 61 - 70 | 71 - 80 | 81 - 90 | 91 - 100 |
| 51² = 2.601 52² = 2.704 53² = 2.809 54² = 2.916 55² = 3.025 56² = 3.136 57² = 3.249 58² = 3.364 59² = 3.481 60² = 3.600 | 61² = 3.721 62² = 3.844 63² = 3.969 64² = 4.096 65² = 4.225 66² = 4.356 67² = 4.489 68² = 4.624 69² = 4.761 70² = 4.900 | 71² = 5.041 72² = 5.184 73² = 5.329 74² = 5.476 75² = 5.625 76² = 5.776 77² = 5.929 78² = 6.084 79² = 6.241 80² = 6.400 | 81² = 6.561 82² = 6.724 83² = 6.889 84² = 7.056 85² = 7.225 86² = 7.396 87² = 7.569 88² = 7.744 89² = 7.921 90² = 8.100 | 91² = 8.281 92² = 8.464 93² = 8.649 94² = 8.836 95² = 9.025 96² = 9.216 97² = 9.409 98² = 9.604 99² = 9.801 100² =10.000 |
B. Akar Pangkat Dua atau Akar Kuadrat
Akar kuadrat atau akar pangkat 2 adalah kebalikan dari operasi pangkat 2 atau invers pangkat 2 suatu bilangan. Nilai akar pangkat dua suatu bilangan x adalah y dimana berlaku x² = y dengan x dan y bilangan real. Akar kuadrat disimbolkan dengan √. Jadi hubungan pangkat dua dan akar pangkat dua sebagai berikut x² = y maka kebalikannya √y = y : x = x. Perhatikan contoh berikut ini.
- 5² = 25 maka kebalikanya √25 = 25 : 5 = 5.
- 45² = 2.025 maka kebalikannya √2.025 = 2.025 : 45 = 45.
- 12² = 144 maka kebalikannya √144 = 144 : 12 = 12.
Ada beberapa cara menentukan akar pangkat dua dari suatu bilangan. Berikut ini beberapa cara yang dapat digunakan untuk menentukan akar pangkat dua suatu bilangan.
1. Cara 1
Metode ini bekerja dengan memisahkan 2 digits bilangan yang dihitung. Sebagai catatan cara ini hanya bisa digunakan untuk bilangan kuadrat 100 sampai dengan 10.000
Kita harus ingat bilangan pangkat dua dari 0 sampai 9.
| Pangkat Dua | ||
|---|---|---|
| 0²= 0 1² = 1 2² = 4 3² = 9 | 4² = 16 5² = 25 6² = 36 7² = 49 | 8² = 64 9² = 81 |
Contoh 1 :
√144 = ...
- Pisahkan dua angka dari kanan menjadi 1 dan 44. Bagian kiri 1 dan bagian kanan 44.
- Jawaban digit pertama (puluhan) diperoleh dari bilangan kuadrat yang hasilnya mendekati 1. Berapa kuadrat yang hasilnya mendekati 1? Bilangan kuadrat yang hasilnya mendekati 1 adalah 1² = 1. Jika kita menggunakan 2² hasilnya adalah 4 maka lebih dari 1. Jadi jawaban digit pertamanya adalah 1.
- Selanjutnya bilangan digit kedua (satuan). Kurangkan hasil 1² = 1 dengan 1. 1 - = 0. Sisa hasil pengurangan adalah 0. Bandingkan sisa hasil pengurangan dengan hasil digit pertama, hasilnya lebih besar atau lebih kecil? Ternyata sisa hasil pengurangannya lebih kecil. Karena lebih kecil makan nantinya kita pilih bilangan yang satuannya lebih kecil. Kita lihat angka bagian kanan yaitu 44. Satuannya adalah bilangan 4. Kita cari bilangan kuadrat yang angka satuannya 4 yaitu 2² = 4 dan 8² = 64. Karena hasil pengurangannya tadi lebih kecil digit pertama maka kita ambil yang ekornya kecil. Antara 2 dan 8 lebih kecil 2 sehingga hasil digit kedua adalah 2.
- Jadi √144 = 12
- Catatan jika bilangan kuadrat berakhiran 0 dan 5 maka digit keduanya adalah tetap yaitu 0 dan 5.
Contoh 2 :
√1369 = ...
- Pisahkan dua angka dari kanan menjadi 13 dan 69. Bagian kiri 13 dan bagian kanan 69.
- Jawaban digit pertama (puluhan) diperoleh dari bilangan kuadrat yang hasilnya mendekati 13. Berapa kuadrat yang hasilnya mendekati 13? Bilangan kuadrat yang hasilnya mendekati 13 adalah 3² = 9. Jika kita menggunakan 4² hasilnya adalah 16 maka lebih dari 13. Jadi jawaban digit pertamanya adalah 3.
- Selanjutnya bilangan digit kedua (satuan). Kurangkan hasil 3² = 9 dengan 13. 13 - 9 = 4. Sisa hasil pengurangan adalah 4. Bandingkan sisa hasil pengurangan dengan hasil digit pertama, hasilnya lebih besar atau lebih kecil? Ternyata sisa hasil pengurangannya lebih besar. Karena lebih besar makan nantinya kita pilih bilangan yang satuannya lebih besar. Catatan jika hasil pengurangannya sama besar juga mengambil yang ekornya lebih besar. Kita lihat angka bagian kanan yaitu 69. Satuannya adalah bilangan 9. Kita cari bilangan kuadrat yang angka satuannya 9 yaitu 3² = 9 dan 7² = 49. Karena hasil pengurangannya tadi lebih besar digit pertama maka kita ambil yang ekornya besar. Antara 3 dan 7 lebih besar 7 sehingga hasil digit kedua adalah 7.
- Jadi √1369 = 37
- Catatan jika bilangan kuadrat berakhiran 0 dan 5 maka digit keduanya adalah tetap yaitu 0 dan 5.
Cara yang kedua ini hampir sama dengan cara yang pertama. Langkah-langkahnya antara lain sebagai berikut.
Contoh 1
√144 = ...
- Pisahkan dua angka dari kanan (belakang). Sehingga bilangan sebelah kiri adalah 1 dan sebelah kanan adalah 44.
- Tentukan bilangan kuadrat yang mendekati atau sama dengan bilangan sebelah kiri. Ternyata bilangan yang memenuhi adalah 1² = 1. Kemudian kurangkan sehinggga tersisa angka 44.
- Jumlahkan angka digit pertama (1 + 1 = 2).
- Tentukan angka kembar yang hasil perkalianya mendekati atau sama dengan bilangan tersisa (44). Ternyata bilangan yang memenuhi adalah 22 x 2 = 44. Jadi bilangan digit kedua adalah 2.
- Hasil yang diperoleh adalah √144 =12.
Contoh 2 :
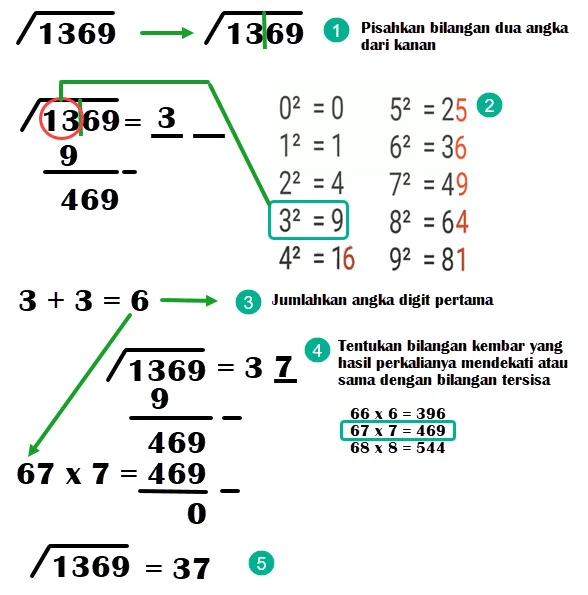
√1369 = ...
- Pisahkan dua angka dari kanan (belakang). Sehingga bilangan sebelah kiri adalah 13 dan sebelah kanan adalah 69.
- Tentukan bilangan kuadrat yang mendekati atau sama dengan bilangan sebelah kiri. Ternyata bilangan yang memenuhi adalah 3² = 9. Kemudian kurangkan sehinggga tersisa angka 469.
- Jumlahkan angka digit pertama (3 + 3 = 6).
- Tentukan angka kembar yang hasil perkalianya mendekati atau sama dengan bilangan tersisa (469). Ternyata bilangan yang memenuhi adalah 67 x 7 = 469. Jadi bilangan digit kedua adalah 7.
- Hasil yang diperoleh adalah √1369=37.
Silahkan masukkan bilangan kuadrat pada kotak, kemudian klik hitung hasilnya akan muncul.
Demikian pembehasan mengenai Bilangan Pangkat Dua dan Akar Pangkat Dua. Semoga tulisan ini bermanfaat.












0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.