n/2, n/2+ 1. Nilai tengahnya adalah nilai pada suku ke n/2 ditambah nilai pada suku n/2 + 1 kemudian dibagi 2. Cara menentukan rata-rata adalah jumlah data dibagi banyak data.
Berikut ini beberapa contoh soal latihan dan pembahasannya tentang materi statistika yang diajarkan di kelas VI sekolah dasar dengan kurikulum 2013. Semoga soal ini dapat menambah pemahaman Anda tentang materi statistika yang telah diajarkan sebelumnya,
1. Jawablah pertanyaan berikut dengan tepat!
Sepuluh orang siswa dijadikan sebagai sampel. Lengkapi dengan pemecahannya. Masing-masing siswa diukur tinggi badannya. Hasil pengukuran tinggi badan adalah
sebagai berikut.
172, 167, 180, 170, 169, 160, 175, 165, 173, 170.
Tentukan rata-rata, nilai tengah, dan modus data yang sering muncul!
Diketahui :
Data berjumlah genap
Urutan data : 160, 165, 167, 169, 170, 170, 172, 173, 175, 180
Banyak data (n) = 10
Jumlah data (F) = 160+165+167+169+170+170+172+173+175+180 = 1.701
Ditanyakan : Rata-rata, Median dan Modus
Jawab :
Rata-rata adalah :
| x̄ = | F |
| n |
| x̄ = | 1.701 |
| 10 |
Jadi, rata-rata tinggi badan siswa adalah 170,1
Karena data berjumlah genap maka median data adalah :
| Me = | 1 | (x ( | n | ) + x ( | n | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x ( | 10 | ) + x ( | 10 | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x5 + x6) |
| 2 |
Dari pengurutan diatas diperoleh nilai x5 sama dengan 170 dan x6 sama dengan 170. Dengan demikian penghitungan median dapat dilanjutkan.
| Me = | 1 | (170 + 170) |
| 2 |
| Me = | 1 | (340) |
| 2 |
Jadi median data adalah 170.
Modus dalam data tersebut adalah 170, karena 170 merupakan data yang paling sering muncul yaitu sebanyak 2 kali, sedangkan angka lainnya hanya satu kali.
Jadi, rata - rata = 170,1 median (nilai tengah) = 170 dan modus = 170
2. Delapan mobil sedang melaju di suatu jalan raya. Kecepatan kedelapan mobil tersebut
adalah seperti berikut.
60 , 80, 70, 50, 60, 70, 45, 75
Tentukan modus kecepatan mobil!
Diketahui :
Urutan data : 45, 50, 60, 60, 70, 70, 75, 80
Ditanyakan : Modus data
Jawab
Madus adalah data yang paling sering muncul yaitu 60 dan 70.
3. Delapan orang siswa memiliki nilai ujian sebagai berikut.
77, 62, 72, 54, 76, 57, 81, 70
Tentukan rata-rata nilai ujian siswa.
Diketahui :
Banyak data (n) = 8
Urutan data = 54, 57, 62, 70, 72, 76, 77, 81
Jumlah data (F) = 54+57+62+70+72+76+77+81 = 549
Ditanyakan : Rata-rata nilai ujian
Jawab :
| x̄ = | F |
| n |
| x̄ = | 79 |
| 8 |
Jadi, rata-rata nilai ujian siswa adalah 68,625.
4. Jumlah kematian pada bayi seperti terlihat pada tabel.
Pada tahun berapa angka kematian pada bayi meningkat?
Diketahui :
Tahun 2014 = 500 bayi
Tahun 2015 = 400 bayi
Tahun 2016 = 200 bayi
Tahun 2017 = 700 bayi
Ditanyakan : Tahun kenaikan kematian bayi
Jawah :
Antara tahun 2016 dan 2017 terjadi kenaikan kematian bayi sejumlah 500 bayi.
5. Nilai ulangan IPA dari 25 siswa Kelas 6 adalah
7, 6, 5, 5, 7, 8, 7, 8, 7, 9, 5, 7, 6,
5, 9, 8, 5, 6, 7, 8, 9, 6, 5, 7, 4
a. Tentukan nilai rata-ratanya
b. Tentukan modusnya.
Diketahui :
Tabel distribusi frekuensi data :
Banyak data (n) = 25
Jumlah data (F)= 166
Rata-rata data adalah :
x̄ = 6,64
Jadi, rata-rata nilai ulangan siswa adalah 6,69.
Modus adalah data yang paling sering muncul yaitu 7 muncul sebanyak tujuh kali.
6. Rudi, Eka, dan Indra sedang menanyakan tentang olahraga yang digemari siswa
kelas VI SD Cemerlang. Hasil yang diperoleh dicatat dalam tabel berikut.
Tentukan modus dari data di atas.
Modus data adalah sepakbola karena muncul sebanyak 10 kali
7. Data berat badan siswa kelas VI SD Harapan Bangsa seperti berikut.
32, 34, 34, 33, 34, 33, 32, 35, 34, 32,
33, 34, 34, 32, 33, 34, 32, 33, 33, 34
Tentukan rata-rata, nilai tengah, dan data yang sering muncul!
Diketahui :
Urutan data : 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 34, 34, 34, 34, 34, 34, 34, 34, 35.
Tabel distribusi frekuensi :
Banyak data (n) = 20
Jumlah data (F) = 665
Ditanyakan rata-rata :
x̄ = 33,25
Jadi, rata-rata barat badansiswa adalah 33,25
Median data adalah :
Karena data berjumlah genap maka median data adalah :
Untuk melanjutkan penghitungan, kita harus terlebih dahulu mengetahui nilai x10 dan x11.
Dari pengurutan diatas diperoleh nilai x10 sama dengan 33 dan x11 sama dengan 33. Dengan demikian penghitungan median dapat dilanjutkan.
Me = 33
Jadi median data adalah 33.
Modus adalah data yang paling sering muncul yaitu 34 (muncul sebanyak 8 kali)
8. Diagram batang di bawah ini menunjukkan banyak buku yang dipinjam di
perpustakaan Kota Malang. Hal ini terjadi dari tahun 2014 sampai dengan 2017.
Datanya sebagai berikut
Diketahui :
Tahun 2014 = 300
Tahun 2015 = 400
Tahun 2016 = 500
Tahun 2017 = 600, maka
a. Berapa jumlah buku yang dipinjam dari tahun 2014 hingga 2017?
Jawab : 300+400+500+600=1.800
b. Berapa rata-rata buku yang dipinjam dalam satu tahun?
Banyak data (n) =4
Jumlah data (F) = 1.800
Ditanyakan rata-rata :
x̄ = 450
Jadi, rata-rata peminjaman buku per tahun adalah 450.
c. Tahun berapakah paling banyak buku di perpustakaan Kota Malang yang dipinjam? Tahun 2017
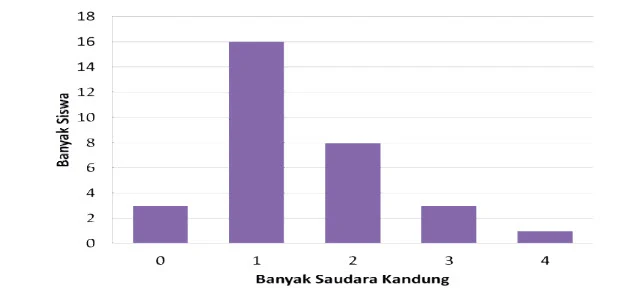
9. Edo mendata banyak saudara kandung dari teman-teman sekelasnya. Data tersebut
seperti terlihat pada diagram batang berikut.
Diketahui :
Jumlah saudara 0 = 2
Jumlah saudara 1 = 16
Jumlah saudara 2 = 8
Jumlah saudara 3 = 3
Jumlah saudara 4 = 1
a. Berapa rata-rata banyak saudara kandung dari teman-teman sekelasnya Edo?
Banyak data (n) = 5
Jumlah data (F) = (2+16+8+3+1) = 29
Ditanyakan rata-rata :
x̄ = 5,8
Jadi, rata-rata jumlah saudara teman edo adalah 5,8.
b. Berapa banyak saudara kandung yang banyak dimiliki teman Edo? Modus data adalah saudara yang berumur 1 tahun (muncul 16 kali)
10. Perhatikan data pada tabel berikut!
Tentukan rata-rata, median, dan modus dari data di atas.
Diketahui :
Urutan data : 60, 65, 65, 65, 65, 70, 70, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 85, 85,85, 90, 95
Tabel distribusi frekuensi
Banyak data (n) = 33
Jumlah data (F) = 665
Ditanyakan :
Rata-rata ;
x̄ = 76,66
Jadi, rata-rata nilai adalah 76,66
Median :
Data ganjil
Me = x17
Dari hasil pengurutan dapat kita ketahui mediannya (x17) adalah 75.
Modus adalah data yang paling sering muncul yaitu 80 (muncul 11 kali).
11. Berikut ini data ukuran sepatu dari 25 pemain sepak bola.
39 37 39 37 41
38 40 39 38 41
38 40 40 39 42
40 41 42 38 40
41 41 40 38 39
Modus dari data di atas adalah . . . .
Diketahui :
Urutan data : 37, 37, 38, 38, 38, 38, 38, 39, 39, 39, 39, 39, 40, 40, 40, 40, 40, 40, 41, 41, 41, 41, 41. 42, 42
Ditanyakan Modus
Modus data adalah 40 (muncul 6 kali)
12. Tabel berikut menunjukkan banyak penjualan mobil di showroom JAYA.
Hitung modus penjualan jenis mobil berdasarkan tabel di atas!
Modus penjualan mobil showroom JAYA adalah jeep.
13. Diketahui tinggi badan dari 10 siswa adalah 145, 143, 146, 140, 144, 139, 143, 141, 145,
140. Tentukan median dari data tinggi badan tersebut?
Diketahui :
Jumlah data : genap (10)
Urutan data : 139, 140, 140, 141, 143, 143, 144, 145, 145, 146
Ditanyakan : Median
Untuk melanjutkan penghitungan, kita harus terlebih dahulu mengetahui nilai x5 dan x6.
Dari pengurutan diatas diperoleh nilai x5 sama dengan 143 dan x6 sama dengan 143. Dengan demikian penghitungan median dapat dilanjutkan.
Me = 143
Jadi median data adalah 143.
14. Berat badan 15 anak adalah sebagai berikut. Satuannya dalam kg.
35, 37, 40, 29, 36, 35, 38, 30, 36, 40, 36, 30, 32, 35, 39
Berapa median dari data tinggi badan tersebut?
Diketahui :
Data berjumlah ganjil
Urutan data : 29,30,30,32,35,35,35,36,36,36,37,38,39,40,40
Ditanyakan : Median
Me = x8
Dari hasil pengurutan dapat kita ketahui mediannya (x8) adalah 36.
Jadi median data adalah 36.
15. Berat 10 buah melon dari hasil panen pak Udin sebagai berikut. Satuannya dalam kg.
3, 2, 3, 5, 4, 2, 3, 3, 2, 3
Berapa banyak buah melon yang memiliki berat lebih dari rata-rata?
Diketahui :
Banyak data =
Jumlah data (F) = 3+2+3+5+4+2+3+3+2+3 = 30
Ditanyakan : Melon di atas rata-rata
x̄ = 3
Jadi, rata-rata nilai adalah 3 sehingga berat melon di atas 3 kg ada 2 buah yaitu melon dengan berat 4 dan 5 kg.
16. Pak Wayan mempunyai 6 ekor sapi. Rata-rata berat satu ekor sapi adalah 460 kg. Berat kelima sapi adalah 475 kg, 490 kg, 430 kg, 420 kg, dan 460 kg. Tentukan berat sapi keenam!
Diketahui :
Rata-rata berat 6 ekor sapi = 460
Jumlah berat lima ekor sapi = 475+490+430+420+460 = 2.275
Ditanya : Berat sapi keenam
Penyelesaian :
Berat sapi keenam = (6 x 460) - 2.275
Tinggi badan Beni = 2.760 - 2.275
Tinggi badan Beni = 485 kg
Jadi berat sapi keenam adalah 485 kg.
17. Diketahui beberapa nomor sepatu teman-teman Edo. Data tersebut adalah
37, 38, 35, 36, 37, 40, 39, 36, 36, 35
Tentukan nilai yang tepat untuk mewakili di antara modus, median, dan mean!
Diketahui :
Data berjumlah genap yaitu 10
Urutan data : 35, 35, 36, 36, 36, 37, 37, 38, 39, 40
Banyak data (n) = 10
Jumlah data = (35 + 35 + 36 + 36 + 36 + 37 + 37 + 38 + 39 + 40) = 369
Ditanyakan : modus, median dan mean
Modus adalah data yang paling sering muncul yaitu 36 (muncul 3 kali)
Median :
Karena data berjumlah genap maka median data adalah :
Untuk melanjutkan penghitungan, kita harus terlebih dahulu mengetahui nilai x5 dan x6.
Dari pengurutan diatas diperoleh nilai x5 sama dengan 36 dan x6 sama dengan 37. Dengan demikian penghitungan median dapat dilanjutkan.
Me = 36,5
Jadi median data adalah 36,5
Mean :
x̄ = 36,9
Jadi, rata-rata nilai adalah 36,9
Jadi modus, median dan mean dapat mewakili data dengan tepat.
18. Ayah Beni, membeli beberapa buah-buahan. Buah yang dibeli, antara lain 5 buah mangga, 6 buah apel, dan 7 buah manggis. Manakah nilai yang tepat mewakili di antara modus, median, dan mean?
Modusnya adalah manggis (7) dan tidak memiliki median dan rata-rata sehingga yang dapat mewakili dengan tepat adalah modus.
19. Ada beberapa data disajikan berikut.
500, 3, 3
Tentukan nilai yang tepat mewakili di antara modus, median dan mean!
Diketahui :
Urutan data : 3, 3, 500
Data berjumlah ganjil
Banyak data (n) = 3
Jumlah data (F) = 506
Ditanyakan : Nilai yang tepat mewakili modus, median, dan mean.
Jawab :
Modus adalah 3 (muncul 2 kali)
Median adalah 3
Mean :
x̄ = 168,67
Jadi, rata-rata nilai adalah 168,67
Sehingga yang dapat mewakili tepat data adalah rata-rata, sedangkan modus dan median datanya terlelu kecil.
20. Tentukanlah nilai yang tepat mewakili di antara modus, median, dan mean pada data
berikut!
400, 5, 400, 5
Tentukan nilai yang tepat mewakili di antara modus, median, dan mean pada data di
atas!
Diketahui :
Urutan data : 5, 5, 400, 400
Data genap (4)
Banyak data (n) = 4
Jumlah data (F) = 810
Ditanyakan : Nilai yang tepat mewakili modus, median dan mean
Jawab :
Modus tidak ada
Median :
Karena data berjumlah genap maka median data adalah :
Untuk melanjutkan penghitungan, kita harus terlebih dahulu mengetahui nilai x2 dan x3.
Dari pengurutan diatas diperoleh nilai x2 sama dengan 5 dan x3 sama dengan 400. Dengan demikian penghitungan median dapat dilanjutkan.
Me = 202,5
Jadi median data adalah 202,5
Mean :
Mean :
x̄ = 202,5
Jadi, rata-rata nilai adalah 202,5
Sehingga yang dapat mewakili tepat data adalah median dan mean, sedangkan modusnya tidak ada.
Diketahui :
Tahun 2014 = 500 bayi
Tahun 2015 = 400 bayi
Tahun 2016 = 200 bayi
Tahun 2017 = 700 bayi
Ditanyakan : Tahun kenaikan kematian bayi
Jawah :
Antara tahun 2016 dan 2017 terjadi kenaikan kematian bayi sejumlah 500 bayi.
5. Nilai ulangan IPA dari 25 siswa Kelas 6 adalah
7, 6, 5, 5, 7, 8, 7, 8, 7, 9, 5, 7, 6,
5, 9, 8, 5, 6, 7, 8, 9, 6, 5, 7, 4
a. Tentukan nilai rata-ratanya
b. Tentukan modusnya.
Diketahui :
Tabel distribusi frekuensi data :
| Nilai | Banyaknya Siswa | Jumlah |
|---|---|---|
| 4 | 1 | 4 |
| 5 | 6 | 30 |
| 6 | 4 | 24 |
| 7 | 7 | 49 |
| 8 | 4 | 32 |
| 9 | 3 | 27 |
| Jumlah Keseluruhan | 25 | 166 |
Jumlah data (F)= 166
Rata-rata data adalah :
| x̄ = | F |
| n |
| x̄ = | 166 |
| 25 |
Jadi, rata-rata nilai ulangan siswa adalah 6,69.
Modus adalah data yang paling sering muncul yaitu 7 muncul sebanyak tujuh kali.
6. Rudi, Eka, dan Indra sedang menanyakan tentang olahraga yang digemari siswa
kelas VI SD Cemerlang. Hasil yang diperoleh dicatat dalam tabel berikut.
| Jenis Olah Raga | Banyak Siswa |
|---|---|
| Bulutangkis | 4 |
| Renang | 5 |
| Sepak Bola | 10 |
| Voli | 6 |
| Kasti | 3 |
Modus data adalah sepakbola karena muncul sebanyak 10 kali
7. Data berat badan siswa kelas VI SD Harapan Bangsa seperti berikut.
32, 34, 34, 33, 34, 33, 32, 35, 34, 32,
33, 34, 34, 32, 33, 34, 32, 33, 33, 34
Tentukan rata-rata, nilai tengah, dan data yang sering muncul!
Diketahui :
Urutan data : 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 34, 34, 34, 34, 34, 34, 34, 34, 35.
Tabel distribusi frekuensi :
| Berat Badan | Banyaknya Siswa | Jumlah |
|---|---|---|
| 32 | 5 | 160 |
| 33 | 6 | 198 |
| 34 | 8 | 272 |
| 35 | 1 | 35 |
| Jumlah Keseluruhan | 20 | 665 |
Jumlah data (F) = 665
Ditanyakan rata-rata :
| x̄ = | F |
| n |
| x̄ = | 665 |
| 20 |
Jadi, rata-rata barat badansiswa adalah 33,25
Median data adalah :
Karena data berjumlah genap maka median data adalah :
| Me = | 1 | (x ( | n | ) + x ( | n | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x ( | 20 | ) + x ( | 20 | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x10 + x11) |
| 2 |
Dari pengurutan diatas diperoleh nilai x10 sama dengan 33 dan x11 sama dengan 33. Dengan demikian penghitungan median dapat dilanjutkan.
| Me = | 1 | (33 + 33) |
| 2 |
| Me = | 1 | (66) |
| 2 |
Jadi median data adalah 33.
Modus adalah data yang paling sering muncul yaitu 34 (muncul sebanyak 8 kali)
8. Diagram batang di bawah ini menunjukkan banyak buku yang dipinjam di
perpustakaan Kota Malang. Hal ini terjadi dari tahun 2014 sampai dengan 2017.
Datanya sebagai berikut
Diketahui :
Tahun 2014 = 300
Tahun 2015 = 400
Tahun 2016 = 500
Tahun 2017 = 600, maka
a. Berapa jumlah buku yang dipinjam dari tahun 2014 hingga 2017?
Jawab : 300+400+500+600=1.800
b. Berapa rata-rata buku yang dipinjam dalam satu tahun?
Banyak data (n) =4
Jumlah data (F) = 1.800
Ditanyakan rata-rata :
| x̄ = | F |
| n |
| x̄ = | 1.800 |
| 4 |
Jadi, rata-rata peminjaman buku per tahun adalah 450.
c. Tahun berapakah paling banyak buku di perpustakaan Kota Malang yang dipinjam? Tahun 2017
9. Edo mendata banyak saudara kandung dari teman-teman sekelasnya. Data tersebut
seperti terlihat pada diagram batang berikut.
Diketahui :
Jumlah saudara 0 = 2
Jumlah saudara 1 = 16
Jumlah saudara 2 = 8
Jumlah saudara 3 = 3
Jumlah saudara 4 = 1
a. Berapa rata-rata banyak saudara kandung dari teman-teman sekelasnya Edo?
Banyak data (n) = 5
Jumlah data (F) = (2+16+8+3+1) = 29
Ditanyakan rata-rata :
| x̄ = | F |
| n |
| x̄ = | 29 |
| 4 |
Jadi, rata-rata jumlah saudara teman edo adalah 5,8.
b. Berapa banyak saudara kandung yang banyak dimiliki teman Edo? Modus data adalah saudara yang berumur 1 tahun (muncul 16 kali)
10. Perhatikan data pada tabel berikut!
| Nilai | Banyak Siswa |
|---|---|
| 60 | 1 |
| 65 | 4 |
| 70 | 2 |
| 75 | 10 |
| 80 | 11 |
| 85 | 3 |
| 90 | 1 |
| 95 | 1 |
Diketahui :
Urutan data : 60, 65, 65, 65, 65, 70, 70, 75, 75, 75, 75, 75, 75, 75, 75, 75, 75, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 80, 85, 85,85, 90, 95
Tabel distribusi frekuensi
| Nilai | Banyaknya Siswa | Jumlah |
|---|---|---|
| 60 | 1 | 60 |
| 65 | 4 | 260 |
| 70 | 2 | 140 |
| 75 | 10 | 750 |
| 80 | 11 | 880 |
| 85 | 3 | 255 |
| 90 | 1 | 90 |
| 95 | 1 | 95 |
| Jumlah | 33 | 2.530 |
Jumlah data (F) = 665
Ditanyakan :
Rata-rata ;
| x̄ = | F |
| n |
| x̄ = | 2.530 |
| 33 |
Jadi, rata-rata nilai adalah 76,66
Median :
Data ganjil
| Me = x | (n + 1) |
| 2 |
| Me = x | (33 + 1) |
| 2 |
| Me = x | (34) |
| 2 |
Dari hasil pengurutan dapat kita ketahui mediannya (x17) adalah 75.
Modus adalah data yang paling sering muncul yaitu 80 (muncul 11 kali).
11. Berikut ini data ukuran sepatu dari 25 pemain sepak bola.
39 37 39 37 41
38 40 39 38 41
38 40 40 39 42
40 41 42 38 40
41 41 40 38 39
Modus dari data di atas adalah . . . .
Diketahui :
Urutan data : 37, 37, 38, 38, 38, 38, 38, 39, 39, 39, 39, 39, 40, 40, 40, 40, 40, 40, 41, 41, 41, 41, 41. 42, 42
Ditanyakan Modus
Modus data adalah 40 (muncul 6 kali)
12. Tabel berikut menunjukkan banyak penjualan mobil di showroom JAYA.
| No | Jenis Mobil | Jumlah |
|---|---|---|
| 1. | Minibus | 15 |
| 2. | Jeep | 32 |
| 3. | Pickup | 18 |
| 4. | Truk | 28 |
| 5 | Sedan | 5 |
Modus penjualan mobil showroom JAYA adalah jeep.
13. Diketahui tinggi badan dari 10 siswa adalah 145, 143, 146, 140, 144, 139, 143, 141, 145,
140. Tentukan median dari data tinggi badan tersebut?
Diketahui :
Jumlah data : genap (10)
Urutan data : 139, 140, 140, 141, 143, 143, 144, 145, 145, 146
Ditanyakan : Median
| Me = | 1 | (x ( | n | ) + x ( | n | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x ( | 10 | ) + x ( | 10 | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x5 + x6) |
| 2 |
Dari pengurutan diatas diperoleh nilai x5 sama dengan 143 dan x6 sama dengan 143. Dengan demikian penghitungan median dapat dilanjutkan.
| Me = | 1 | (143 + 143) |
| 2 |
| Me = | 1 | (286) |
| 2 |
Jadi median data adalah 143.
14. Berat badan 15 anak adalah sebagai berikut. Satuannya dalam kg.
35, 37, 40, 29, 36, 35, 38, 30, 36, 40, 36, 30, 32, 35, 39
Berapa median dari data tinggi badan tersebut?
Diketahui :
Data berjumlah ganjil
Urutan data : 29,30,30,32,35,35,35,36,36,36,37,38,39,40,40
Ditanyakan : Median
| Me = x | (n + 1) |
| 2 |
| Me = x | (15 + 1) |
| 2 |
| Me = x | (16) |
| 2 |
Dari hasil pengurutan dapat kita ketahui mediannya (x8) adalah 36.
Jadi median data adalah 36.
15. Berat 10 buah melon dari hasil panen pak Udin sebagai berikut. Satuannya dalam kg.
3, 2, 3, 5, 4, 2, 3, 3, 2, 3
Berapa banyak buah melon yang memiliki berat lebih dari rata-rata?
Diketahui :
Banyak data =
Jumlah data (F) = 3+2+3+5+4+2+3+3+2+3 = 30
Ditanyakan : Melon di atas rata-rata
| x̄ = | F |
| n |
| x̄ = | 30 |
| 10 |
Jadi, rata-rata nilai adalah 3 sehingga berat melon di atas 3 kg ada 2 buah yaitu melon dengan berat 4 dan 5 kg.
16. Pak Wayan mempunyai 6 ekor sapi. Rata-rata berat satu ekor sapi adalah 460 kg. Berat kelima sapi adalah 475 kg, 490 kg, 430 kg, 420 kg, dan 460 kg. Tentukan berat sapi keenam!
Diketahui :
Rata-rata berat 6 ekor sapi = 460
Jumlah berat lima ekor sapi = 475+490+430+420+460 = 2.275
Ditanya : Berat sapi keenam
Penyelesaian :
Berat sapi keenam = (6 x 460) - 2.275
Tinggi badan Beni = 2.760 - 2.275
Tinggi badan Beni = 485 kg
Jadi berat sapi keenam adalah 485 kg.
17. Diketahui beberapa nomor sepatu teman-teman Edo. Data tersebut adalah
37, 38, 35, 36, 37, 40, 39, 36, 36, 35
Tentukan nilai yang tepat untuk mewakili di antara modus, median, dan mean!
Diketahui :
Data berjumlah genap yaitu 10
Urutan data : 35, 35, 36, 36, 36, 37, 37, 38, 39, 40
Banyak data (n) = 10
Jumlah data = (35 + 35 + 36 + 36 + 36 + 37 + 37 + 38 + 39 + 40) = 369
Ditanyakan : modus, median dan mean
Modus adalah data yang paling sering muncul yaitu 36 (muncul 3 kali)
Median :
Karena data berjumlah genap maka median data adalah :
| Me = | 1 | (x ( | n | ) + x ( | n | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x ( | 10 | ) + x ( | 10 | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x5 + x6) |
| 2 |
Dari pengurutan diatas diperoleh nilai x5 sama dengan 36 dan x6 sama dengan 37. Dengan demikian penghitungan median dapat dilanjutkan.
| Me = | 1 | (36 + 37) |
| 2 |
| Me = | 1 | (73) |
| 2 |
Jadi median data adalah 36,5
Mean :
| x̄ = | F |
| n |
| x̄ = | 369 |
| 10 |
Jadi, rata-rata nilai adalah 36,9
Jadi modus, median dan mean dapat mewakili data dengan tepat.
18. Ayah Beni, membeli beberapa buah-buahan. Buah yang dibeli, antara lain 5 buah mangga, 6 buah apel, dan 7 buah manggis. Manakah nilai yang tepat mewakili di antara modus, median, dan mean?
Modusnya adalah manggis (7) dan tidak memiliki median dan rata-rata sehingga yang dapat mewakili dengan tepat adalah modus.
19. Ada beberapa data disajikan berikut.
500, 3, 3
Tentukan nilai yang tepat mewakili di antara modus, median dan mean!
Diketahui :
Urutan data : 3, 3, 500
Data berjumlah ganjil
Banyak data (n) = 3
Jumlah data (F) = 506
Ditanyakan : Nilai yang tepat mewakili modus, median, dan mean.
Jawab :
Modus adalah 3 (muncul 2 kali)
Median adalah 3
Mean :
| x̄ = | F |
| n |
| x̄ = | 506 |
| 3 |
Jadi, rata-rata nilai adalah 168,67
Sehingga yang dapat mewakili tepat data adalah rata-rata, sedangkan modus dan median datanya terlelu kecil.
20. Tentukanlah nilai yang tepat mewakili di antara modus, median, dan mean pada data
berikut!
400, 5, 400, 5
Tentukan nilai yang tepat mewakili di antara modus, median, dan mean pada data di
atas!
Diketahui :
Urutan data : 5, 5, 400, 400
Data genap (4)
Banyak data (n) = 4
Jumlah data (F) = 810
Ditanyakan : Nilai yang tepat mewakili modus, median dan mean
Jawab :
Modus tidak ada
Median :
Karena data berjumlah genap maka median data adalah :
| Me = | 1 | (x ( | n | ) + x ( | n | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x ( | 4 | ) + x ( | 4 | + 1) ) |
| 2 | 2 | 2 |
| Me = | 1 | (x2 + x3) |
| 2 |
Dari pengurutan diatas diperoleh nilai x2 sama dengan 5 dan x3 sama dengan 400. Dengan demikian penghitungan median dapat dilanjutkan.
| Me = | 1 | (5 + 400) |
| 2 |
| Me = | 1 | (405) |
| 2 |
Jadi median data adalah 202,5
Mean :
Mean :
| x̄ = | F |
| n |
| x̄ = | 810 |
| 4 |
Jadi, rata-rata nilai adalah 202,5
Sehingga yang dapat mewakili tepat data adalah median dan mean, sedangkan modusnya tidak ada.











Nag
ReplyDeleteFagadauda