Pada pembelajaran matematika kelas V sekolah dasar kurikulum merdeka semester 2 terdapat pembahasan tentang perbandingan pada bab 18. Tujuan kegiatan pembelajaran kali ini adalah peserta didik mampu menemukan dua kuantitas yang berubah saat memindahkan 100 jeruk ke dalam keranjang. Menyatakan hubungan antara dua kuantitas yang berubah dengan kalimat matematika menggunakan kotak dan lingkaran.
1. Kadek dan saudaranya mendapatkan kiriman 100 buah jeruk bali dari Nenek. Kemudian mereka memindahkan jeruk tersebut dari kotak ke keranjang.
① Buatlah gambar dari situasi ini.
② Tuliskan banyaknya jeruk di dalam kotak, banyaknya jeruk dalam keranjang, dan jumlah total pada sebuah tabel.
③ Ketika mereka memindahkan jeruk dari kotak ke keranjang, kuantitas mana yang berubah bersama? Kuantitas mana yang tetap tidak berubah?
Kuantitas yang berubah bersama adalah banyak buah jeruk dalam keranjang dan banyak buah jeruk dalam kotak, sedangkan kuantitas yang tidak berubah adalah total buah.
④ Misalkan banyaknya jeruk dalam keranjang ¤ dan banyaknya jeruk dalam kotak Ο, tuliskan kalimat matematika yang menyatakan hubungan antara ¤ dan Ο.
Jika ¤ bertambah maka Ο berkurang
2. Ada beberapa kotak yang bentuk dan ukurannya sama. Tumpuklah kotak-kotak itu di atas papan kayu yang tingginya 10 cm, ukurlah tinggi keseluruhan.
① Buatlah gambar yang sesuai dengan situasi ini.
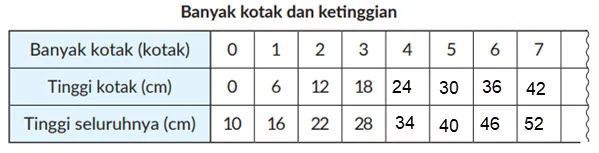
② Tuliskan banyak kotak, tinggi kotak yang ditumpuk, dan tinggi seluruhnya termasuk papan kayu.
③ Ketika kita menumpuk 1 kotak, berapa cm ketinggian bertambah?
Ketinggian bertambah 6 cm
④ Ketika kita menumpuk 7 kotak, berapa cm ketinggian keseluruhannya?
Tinggi keseluruhannya 52 cm
⑤ Ketika kita menumpuk kotak, kuantitas apa yang berubah? Kuantitas mana yang tetap tidak berubah?
Tinggi kotak dan tinggi seluruhnya
⑥ Misalkan banyak kotak ¤ dan ketinggian seluruhnya Ο cm, tuliskan kalimat matematika yang menyatakan hubungan antara ¤ dan Ο.
6 x ¤ + 10 = Ο
⑦ Ayo, menghitung tinggi keseluruhnya untuk 8 kotak dengan menggunakan kalimat matematika tersebut.
6 x 8 + 10 = 58
2. Proporsi
Jika ada dua kuantitas x dan y, dan nilai x menjadi 2 kali, 3 kali, dan seterusnya, nilai y yang sesuai juga menjadi 2 kali, 3 kali, dan seterusnya. Oleh karena itu, y dikatakan sebanding dengan x. Untuk 1/2 kali, 1/3 kali, dan seterusnya (kelipatan pecahan), akan dipelajari pada konten proporsi di kelas 6.
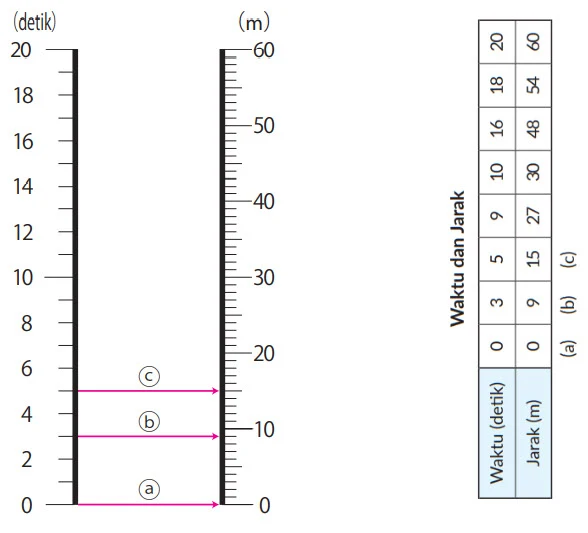
1. Untuk memperingati hari kemerdekaan Republik Indonesia, di kampungkampung diadakan lomba balap karung, yaitu lomba lari di mana pesertanya memakai karung sambil berlari pada lintasan, seperti ditunjukkan pada gambar di atas. Panjang lintasan adalah 60 m. Seorang anak mencatat waktu dan jarak yang ditempuh oleh seorang peserta pada tabel.
① Setelah 3 detik, kita menyatakan bahwa jarak yang telah ditempuh adalah 9 m seperti diagram (b) jaraknya 9 m.
② Berapa m jarak yang telah ditempuh setelah 1 detik?
1 x 3 = 3 m
③ Bagaimana kamu tahu berapa jarak yang telah ditempuh setelah 12 detik dan 15 detik?
Mengalikan dengan 3, 12 x 3 =36 dan 15 x 3 = 45
④ Isilah tabel waktu mulai dari start dan jarak yang telah ditempuh oleh peserta.
Waktu yang dihabiskan mulai dari start adalah ¤ detik dan jarak yang telah ditempuh adalah Ο m. Jika ¤ bertambah, maka Ο juga ikut bertambah.
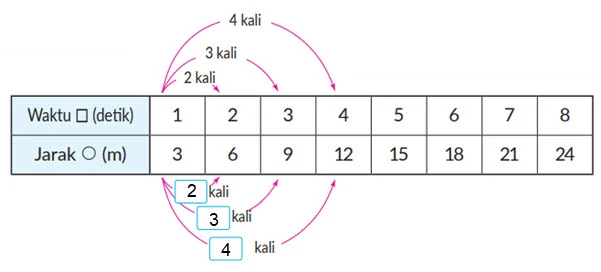
⑤ Ketika waktu ¤ detik bertambah 2 kali, 3 kali, 4 kali, dan seterusnya, kita lihat bagaimana jarak yang ditempuh juga ikut berubah. Isilah kotak di bawah dengan suatu bilangan.
Jika ada dua kuantitas yang berubah, ¤ dan Ο, ¤ berubah menjadi 2 kali, 3 kali dan seterusnya, dan Ο juga berubah menjadi 2 kali, 3 kali, dan seterusnya, maka Ο berbanding lurus (berbanding senilai) dengan ¤.
Latihan
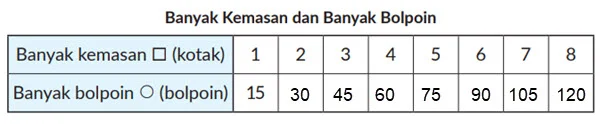
1. Sebuah toko alat tulis menyimpan bolpoin dalam kemasan. Setiap ¤ kemasan berisi 15 bolpoin. Banyaknya bolpoin yang tersedia adalah Ο.
① Jika banyaknya kemasan 1, 2, 3, dan seterusnya, temukan nilai yang bersesuaian dan tuliskan hasilnya pada tabel.
② Sebanding dengan apakah banyaknya bolpoin?
Sebanding dengan banyaknya kemasan
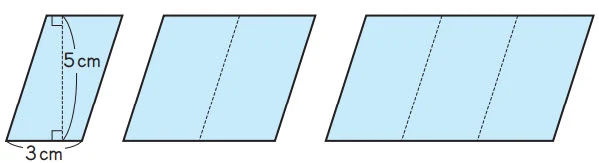
2. Ada sejumlah jajargenjang kongruen yang alasnya 3 cm dan tingginya 5 cm. Dibentuk jajargenjang yang lebih besar dengan menggabungkan mereka seperti ditunjukkan di bawah. Hitunglah luas keseluruhan.
① Tuliskan rumus untuk luas jajargenjang ini dan periksalah manakah 2 unsur yang berubah bersamaan. Lalu unsur apa yang tidak berubah?
Unsur yang berubah adalah alas dan luas
② Tuliskan kalimat matematika dengan menggunakan ¤ cm sebagai alas dan Ο cm2 sebagai luas.
Ο = ¤ x tinggi
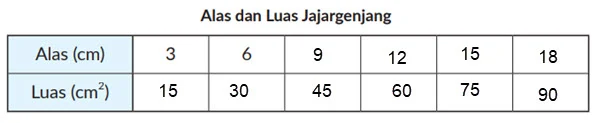
③ Tuliskan hubungan antara alas dan luas dari jajargenjang tersebut pada tabel.
④ Apakah luas jajargenjang sebanding dengan alasnya? Tuliskan alasannya.
Ya karena jika alas bertambah maka luas juga bertambah.
Jika alas jajargenjang adalah x, tingginya a, dan luasnya y, rumus luasnya dapat dinyatakan sebagai y = x × a. Dalam hal ini, jika alas x manjadi 2 kali, 3 kali dan seterusnya, maka luas y juga menjadi 2 kali, 3 kali dan seterusnya, dan terlihat bahwa luas y dari jajargenjang itu sebanding dengan alas x. Selain itu, jika panjang alas tetap konstan dan ketinggian diubah menjadi 2 kali, 3 kali, dan seterusnya, hubungan proporsional dapat ditemukan dengan cara yang sama.
Kondisi dari membuat alas atau tinggi jajargenjang menjadi 2 kali, 3 kali, dan seterusnya, sesuai dengan kondisi dengan manipulasi penyusunan jajargenjang yang kongruen, dan luasnya juga menjadi 2 kali, 3 kali, dan seterusnya yang mudah dipahami secara visual.
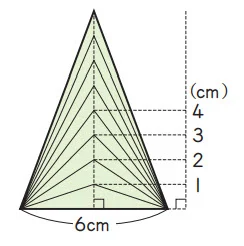
3. Tinggi segitiga dinaikkan sebesar 1 cm seperti ditunjukkan di bawah. Carilah luas masing-masing segitiga.
① Tuliskan rumus untuk luas segitiga dan telitilah unsur manakah yang berubah bersama? Unsur manakah yang tetap?
Luas = alas x tinggi : 2, Unsur yang berubah adalah tinggi dan luas dan yang tetap adalah alas
② Tuliskan hubungan antara tinggi dan luas segitiga pada tabel.
③ Apakah luas segitiga sebanding dengan tingginya? Tuliskan alasannya.
Ya jika tingginya bertambah maka luasnya juga bertambah. Luasnya 3 kali tinggi.
④ Tulislah ekspresi dengan menggunakan ¤ cm sebagai tinggi dan Ο cm2 sebagai luas.
Ο = ¤ × 3
⑤ Jika luas segitiga 30 cm2, berapa cm tingginya?
30 = ¤ × 3¤ = 10
Latihan
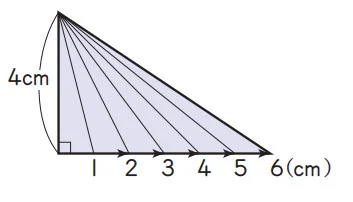
Alas segitiga siku-siku diperpanjang dalam beberapa langkah seperti ditunjukkan di bawah.\\
① Tulislah hubungan antara alas dan luas segitiga pada sebuah tabel.
② Jika luasnya 16 cm2, berapa cm alasnya?
Demikian pembahasan mengenai Perubahan Dua Kuantitas dan Poporsi. Semoga tulisan ini bermanfaat.16 = ¤ × 2, ¤ = 8
Sumber : Buku Matematika Kelas V Unit 2 Kurikulum Merdeka, Kemendikbud















0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.