Pada pembelajaran Matematika Kelas V Sekolah Dasar Kurikulum Merdeka Bab 4 Kekongruenan dan Sudut dari Bangun Datar terdapat kegiatan pembahasan mengenai Sudut dari Bangun Segi banyak. Tujuan kegiatan pembelajaran kali ini adalah peserta didik dapat mencari jumlah sudut dalam dari poligon dan merangkum jumlah sudut dalam dari poligon.
Suatu bangun datar yang hanya dikelilingi oleh garis lurus seperti segitiga, segi empat, segi lima, segi enam, dan seterusnya disebut segi banyak. Dalam suatu segi banyak, tiap garis lurus yang menghubungkan dua titik sudut yang tidak berdekatan disebut diagonal.
Segienam dapat disederhanakan sebagai segitiga kongruen atau segiempat kongruen yang dikelompokkan.Tetapi, seperti segitiga dan segiempat, keduanya tidak dapat disusun dengan cara apa pun, sehingga tidak akan cocok untuk mencari jumlah besar sudutnya.
Suatu segi lima adalah bangun datar dengan 5 sisi.
1. Ayo cari bagaimana cara menemukan jumlah kelima sudut pada segi lima?
1. Dapatkah kamu menggunakan pengubinan?
Untuk kasus segi lima, tidak dapat digunakan pengubinan. Untuk melakukan pengubinan suatu bangun datar, jumlah sudut-sudut yang bertemu pada satu titik sudut adalah 360°. Pada bangun segilima sudutnya tidak bisa digabungkan/disusun, maka besar sudutnya lebih besar dari 360°
2. Ayo bagilah suatu segi lima menjadi segitiga-segitiga.
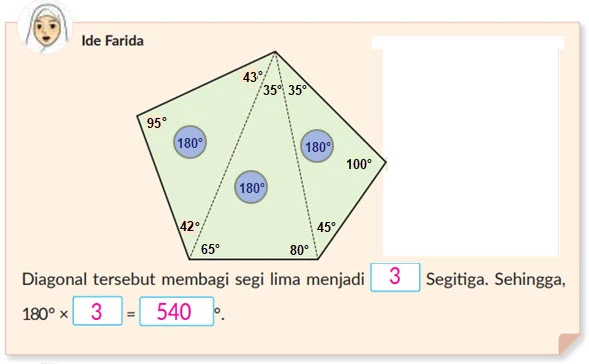
Ide Farida
Menggambar diagonal-diagonal dari suatu titik sudut.
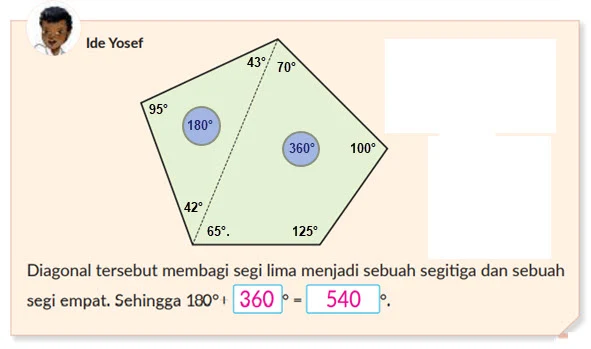
Ide Yosef
Menggambar salah satu diagonal.
Dalam suatu segi lima, jumlah kelima sudutnya adalah 540°
Suatu segi enam adalah bangun datar dengan 6 sisi.
10. Ayo cari bagaimana cara menemukan jumlah keenam sudut pada segi enam.
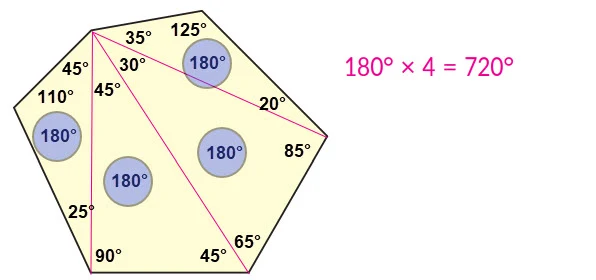
Beberapa cara membagi segienam :
Membagi menjadi 4 segitiga. 180° x 4 = 720°Membagi menjadi segitiga dan segilima. 180° + 540° = 720°Membagi menjadi 6 segitiga 180° x 6 =1080°. 1080° - 360° = 720°Membagi menjadi 2 segiempat 360° x 2 = 720°
11. Simpulkan hubungan antara jumlah sudut pada segi banyak dengan mengisi tabel di bawah ini.
| Bangun | Segi 3 | Segi 4 | Segi 5 | Segi 6 | Segi 7 | Segi 8 | Segi 9 |
|---|---|---|---|---|---|---|---|
| Banyaknya segitiga yang dapat dibuat oleh diagonal-diagonal melalui sebuah titik sudut pada segi banyak | - | 2 | 3 | 4 | 5 | 6 | 7 |
| Jumlah sudut | 180° | 360° | 540° | 720° | 900° | 1080° | 1260° |
Jumlah segitiga bertambah satu dan jumlah segitiga itu lebih sedikit 2 buah dari jumlah titik pada poligon. Jumlah sudut dalam pada n - diagon = 180° x (n-2). Misal pada bangun segilima : 180° x (n-2)= 180° x (5-2) = 180° x 3 = 540°
Sudut yang berhadapan dalam jajargenjang
12. Ayo gunakan apa yang telah kamu pelajari untuk menjelaskan bahwa sudut yang berhadapan dalam jajargenjang besarnya sama.
Karena dua segitiga tersebut kongruen, maka sudut yang berlawanan memiliki besar sudut yang sama.
LATIHAN
1. Ayo hitunglah dan isilah kotak dengan suatu bilangan.
Temukan besar sudut menggunakan jumlah sudut dalam pada poligon.Hitung besar sudut dalam dari segitiga, segiempat, pentagon, dan heksagon
① jumlah besar sudut pada segitiga adalah 180°, temukan besar sudut yang belum ditemukan!
180°−(70°-40°)
② Jumlah dua sudut dalam dan besar sudut luar adalah sama, temukan besar dari sudut luarnya!
180°−40°=140°180°−(140°+15°)
③ Jumlah besar sudut pada segiempat adalah 360o, temukan besar sudut yang belum ditemukan!
360°−(90°+70°+90°)
④ Jumlah besar sudut pada pentagon adalah 540o, temukan besar sudut yang belum ditemukan!
540° − (110° + 125° + 90° + 120°)
⑤ Temukan besar sudut dalam pada sebuah heksagon, dengan mengacu pada besar 3 sudut pada segitiga sama sisi adalah sama!
720° : 6 = 120°
Demikian pembahasan mengenai Sudut dari Bangun Segi banyak. Semoga tulisan ini bermanfaat.
Sumber : Buku Matematika Kelas V Kurikulum Merdeka, Kemendikbud













Mks kak
ReplyDeleteAku senang banget
ReplyDeleteWow mksh kk
ReplyDelete