Dalam kehidupan sehari-hari banyak benda yang memiliki bentuk kubus dan balok. Benda yang berbentu kubus antara lain dadu, permainan rubik, bak mandi, sedangkan benda yang berbentuk balok diantaranya adalah almari, kotak snack, tempat pensil dan masih banyak yang lainya. Kubus dan balok merupakan bangun ruang yang memiliki beberapa kesamaan, yang membedakan kedua bangun datar tersebut adalah panjang masing-masing rusuknya saja, pada kubus semua rusuknya sama penjang sedangkan balok rusuknya tidak semuanya sama panjang. Kedua bangun tersebut memiliki jumlah sisi, rusuk, dan sudut yang sama.
Unsur-Unsur Kubus dan Balok
Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat. Sedangkan balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda.
Balok dan kubus memiliki beberapa unsur yang membangun kedua bangun ruang tersebut. Unsur-unsur yang membangun kubus dan balok adalah sisi, rusuk, sudut, diagonal bidang dan diagonal ruang.
- Sisi atau bidang kubus dan balok adalah bidang yang membatasi kubus dan balok
- Rusuk kubus dan balok adalah garis potong antara dua sisi bidang kubus dan balok.
- Titik sudut suatu kubus dan balok diartikan sebagai titik pertemuan antara tiga rusuk atau tiga sisi di dalam kubus dan balok.
- Diagonal bidang atau diagonal sisi pada kubus dan balok adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan pada setiap bidang atau sisi kubus atau balok.
- Diagonal ruang adalah ruas garis yang menghubungkan dua titik sudut yang berhadapan dalam suatu ruang di dalam bangun kubus dan balok.
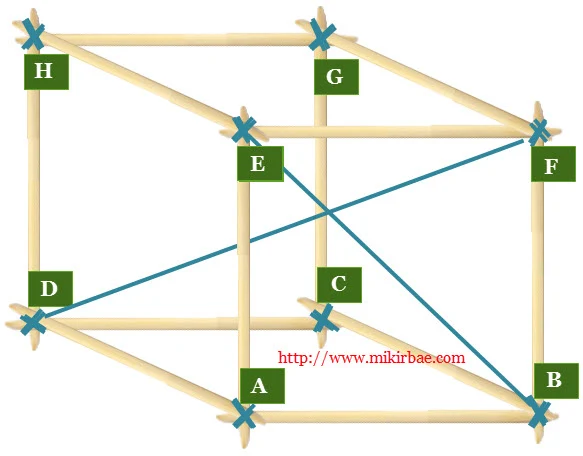
| Nama Bangun | Unsur | |
|---|---|---|
| Kubus | Sisi | ABCD (bawah), EFGH (atas), ABEF (depan), CDGH (belakang), BCGF (kanan), dan ADHE (kiri) |
| Rusuk | AB, BC, CD, AD (bawah), EF, FG, GH, EH (atas), AE, BF, CG, dan DH. | |
| Titik Sudut | <A, <B, <C, <D, <E, <F, <G, <H | |
| Diagonal sisi | AF, BE (depan), CH, DG (belakang), BG, CF (kanan), AH, ED (kiri), AC, BD (bawah), EG, FH (atas) | |
| Diagonal ruang | AG, BH, CE, dan DF | |
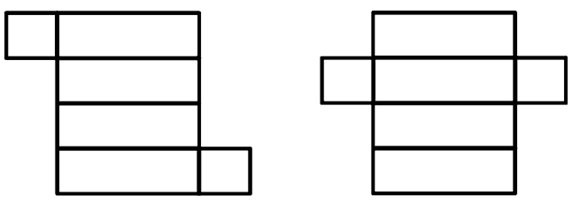
| Jaring-jaring kubus merupakan rangkaian bidang datar (sisi-sisi) yang apabila dipasang atau dirangkaikan akan membentuk sebuah kubus. Jaring-jaring kubus terdiri dari 6 buah persegi yang disusun berdasarkan pola tertentu. Berikut ini beberapa contoh jaring-jaring kubus. | ||
| Balok | Sisi | ABCD (bawah), EFGH (atas), ABEF (depan), CDGH (belakang), BCGF (kanan), dan ADHE (kiri) |
| Rusuk | AB, BC, CD, AD (bawah), EF, FG, GH, EH (atas), AE, BF, CG, dan DH. | |
| Titik Sudut | <A, <B, <C, <D, <E, <F, <G, <H | |
| Diagonal sisi | AF, BE (depan), CH, DG (belakang), BG, CF (kanan), AH, ED (kiri), AC, BD (bawah), EG, FH (atas) | |
| Diagonal ruang | AG, BH, CE, dan DF | |
| Jaring-jaring balok merupakan rangkaian bidang datar (sisi-sisi) yang apabila dipasang atau dirangkaikan akan membentuk sebuah kubus. Jaring-jaring kubus terdiri dari 4 buah persegi panjang dan 2 buah yang disusun berdasarkan pola tertentu. Berikut ini beberapa contoh jaring-jaring balok. | ||
Untuk mengetahui unsur-unsur yang ada dalam kubus dapat dilakukan kegiatan eksplorasi dengan alat dan bahan yang mudah ditemukan di sekitar kita, misalnya saja lidi ataupun sedotan. Alat dan bahan yang diperlukan untuk kegiatan ini antara lain sebagai berikut :
- Alat : Gunting, Lem, Penggaris, Alat tulis, Spidol, Double tape/selotip/lem
- Bahan-bahan: Lidi (tusuk sate) atau sedotan, Benang wol secukupnya, Kalender bekas
Langkah-langkah membuat kerangka kubus dari lidi tusuk sate:
- Ukur lidi (tusuk sate) sepanjang yang dibutuhkan dengan menggunakan penggaris dan alat tulis (lidi sebanyak 12 buah karena kubus terdiri atas 12 buah rusuk).
- Potong lidi tusuk sate yang sudah diukur sama panjang.
- Rekatkan 12 buah lidi tersebut menjadi sebuah kerangka kubus dengan menggunakan lem kayu (atau lem sejenis).
- Setelah terbentuk kerangka kubus, gunakan kertas kalender bekas untuk menulis label A, B, C, D, E, F, G, H dan tempelkan.
Perhatikan kerangka kubus yang telah dibuat. Dari kerangka tersebut, kita dapat menemukan ciri-ciri kubus, yaitu:
- Rusuknya sama panjang
- Sudutnya sama besar
- Jumlah rusuknya 12 buah
- Jumlah bidangnya 6 buah
- Ikatkan ujung benang wol pada sudut B
- Tarik ujung lainnya pada sudut E.
- Benang dari B-E adalah merupakan diagonal bidang
Bagaimana cara mengetahui diagonal ruang pada kubus? Perhatikan gambar kubus berikut! Diagonal ruang pada kubus tersebut adalah garis AG, BH, DF, dan CE. Jika kita tarik benang dari D ke F dan D ke B, maka akan dihasilkan bangun datar baru.
Persamaan kubus dan balok : sama-sama mempunyai 6 sisi, 12 rusuk, 8 titik sudut, 12 diagonal sisi, 4 diagonal ruang. Perbedaan: Kubus semua sisinya berbentuk persegi, sedangkan balok, ada 1 pasang persegi dan 3 pasang sisi berbentuk persegi panjang.












0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.