Luas dan Keliling Jajargenjang dan Trapesium

Dalam kehidupan sehari-hari banyak ditemukan bentuk bangun datar, diantaranya adalah jajargenjang dan trapesium. Contoh benda berbentuk trapesium adalah atap rumah apabila dilihat dari samping, sedangkan contoh jajargenjang adalah kaca pada pintu mobil, dan masih banyak contoh yang lainnya.

Jenis bangun datar bermacam-macam, antara lain persegi, persegi panjang, segitiga, jajar genjang, trapesium, layang-layang, belah ketupat, dan lingkaran. Namun dalam tulisan ini hanya akan dibahas mengenai luas dan keliling jajargenjang dan trapesium. Jajar Genjang adalah segi empat yang sisinya sepasang-sepasang sama panjang dan sejajar. Sedangkan trapesium adalah segi empat yang memiliki tepat sepasang sisi yang sejajar. Berikut ini penjelasan mengenai luas dan keliling kedua bangun datar tersebut.

Ayo Kita Menalar
Kemudian, coba diskusikan dengan kelompok kalian terhadap beberapa kasus berikut.

No	Pertanyaan	Jawaban
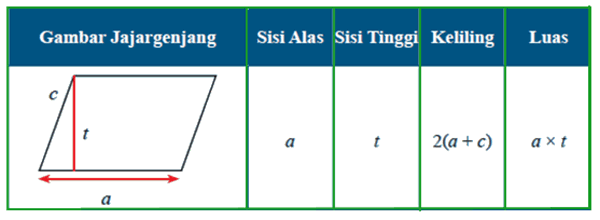
1.	Jika a, t, dan c merupakan alas, tinggi, dan sisi sejajar lainnya pada jajargenjang, maka lengkapilah	Simpulkan hubungan antara Sisi Alas dan Sisi Sejajar yang lain dengan Keliling Keliling jajargenjang didapat dari dua kali dari penjumlahan sisi alas dengan panjang salahsatu sisi sejajar lainnya Jelaskan bagaimana cara menemukan Rumus Luas Jajargenjang (dengan menggunakan konsep luas persegi atau persegipanjang) Perhatikan gambar jajargenjang berikut:
Langkah-langkah menemukan rumus luas jajargenjang adalah sebagai berikut. Tarik garis tinggi DE dan beri ukurannya t satuan sebagai tinggi jajargenjang. Potong segitiga AED dan pindahkan ke kanan menjadi segitiga BCF. Hal ini dapat dilakukan karena jajargenjang memiliki dua pasang sisi sejajar. Perhatikan panjang AB pada jajargenjang ABCD sama panjangnya dengan EF pada persegipanjang EFCD. Berarti luas jajargenjang ABCD sama dengan luas persegipanjang EFCD. Luas persegipanjang EFCD = panjang × lebar = a × t satuan luas. Berarti luas jajargenjang ABCD = a × t. Misalkan ABCD adalah jajargenjang dengan panjang alas a, tinggi t, dan l adalah panjang sisi yang lain, maka : L = a × t K = 2a + 2l L adalah luas daerah jajargenjang dan K adalah keliling jajargenjang
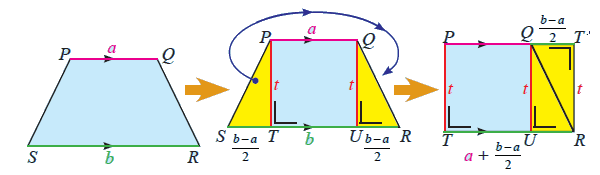
2.	Jika a dan b merupakan panjang dua sisi sejajar pada trapesium dan c merupakan panjang sisi lainnya pada trapesium sama kaki, maka lengkapilah	Simpulkan hubungan antara dua sisi sejajar dan sisi-sisi lainya dengan Keliling Keliling trapesium didapat dari dua kali jumlah sisi sejajar dengan jumlah sisi-sisi lainnya. Jelaskan bagaimana cara menemukan Rumus Luas Trapesium (dengan menggunakan konsep luas persegi atau persegipanjang) Perhatikan gambar trapesium berikut.
Perhatikan trapesium samakaki PQRS di atas. Tinggi trapesium t satuan, panjang alas b satuan dan panjang sisi atas a satuan. Akan ditemukan luas trapesium dengan langkah-langkah berikut. Tarik garis tegak lurus dari titik P ke T dan dari Q ke U. Potonglah segitiga STP dan pindahkan dalam bentuk berlawanan dengan segitiga QUR sehingga terbentuk persegipanjang QURT’, sehingga terbentuk persegipanjang PTRT’. Kalian sudah ketahui sebelumnya cara menentukan luas persegipanjang. Perhatikan persegipanjang PTRT’. Luas trapesium = luas persegipanjang PTRT’ = panjang × lebar = TR × RT’ = (a + b - a ) x t 2 = ( 2a + b - a ) x t 2 Luas Trapesium = ( a + b ) x t 2 Secara umum dapat disimpulkan: Sebuah trapesium samakaki, dengan panjang alas b, sisi atas a, dan tingginya t , luas dan kelilingnya adalah: Luas Trapesium = ( a + b ) x t 2 K = SR + RQ + QP + PS L adalah luas daerah trapesium, K adalah keliling trapesium SR, RQ, QP, dan PS adalah sisi-sisi trapesium.
3.	Buatlah bangun jajargenjang dari kertas HVS atau lainnya (misalkan seperti Gambar 1 pada Tabel 8.7a atau Tabel 8.8a). Selanjutnya guntinglah jajargenjang tersebut menjadi beberapa bagian (minimal dua bagian). Kemudian susunlah bagian-bagian potongan tersebut menjadi bangun trapesium. Bagaimana kalian menentukan keliling dan luas trapesium tersebut? Jelaskan
4.	Buatlah bangun trapesium dari kertas HVS atau lainnya (misalkan seperti Gambar 1 pada Tabel 8.7b atau Tabel 8.8b). Selanjutnya guntinglah trapesium tersebut menjadi beberapa bagian (minimal dua bagian). Kemudian susunlah bagian-bagian potongan tersebut menjadi bangun jajargenjang. Bagaimana kalian menentukan keliling dan luas jajargenjang tersebut? Jelaskan.

Contoh 1

Soal	Jawaban
Perhatikan gambar berikut! Jika AB = 20 cm, BC = 12 cm, BE = 16 dan DC = (2x + 4) cm, maka tentukan! a. Nilai x b. Panjang DC c. Keliling jajargenjang ABCD d. Luas Jajargenjang ABCD	a. AB = DC, maka 20 = 2x + 4 20 – 4 = 2x 16 = 2x 6/2 = x x = 8 b. DC = 2x + 4 dan x = 8, maka DC = 2(8) + 4 = 16 + 4 DC = 20 c. AB = CD = 20 BC = AD = 12, maka K = 2AB + 2BC = 2×20 + 2×12 = 40 + 24 K = 64 cm d. BC = AD = 12, maka L = alas × tinggi = AD × BE = 12 × 16 L = 192 cm²
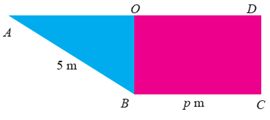
Sebuah model kerangka perahu dibuat dari seng berbentuk persegipanjang yang ditarik menjadi bentuk trapesium siku-siku seperti gambar berikut. Jika panjang OB = 3 m, panjang AB = 5 m, dan panjang BC = p m. Berapa luas persegipanjang sebelum dijadikan model perahu?	Dengan memanfaatkan Dalil Pythagoras diperoleh: AB² = AO² + OB² 5² = AO² + 3² 25 = AO² + 9 AO² = 16 AO = 4 Panjang AD = AO + OD. Karena panjang OD = BC, maka AD = AO + BC. Sehingga diperoleh AD = 4 + p. Dengan demikian, luas persegipanjang mula-mula sebelum dibuat model kapal adalah (p + 4) m².

Ayo Kita Mencoba
Sekarang, coba terapkan pemahaman kalian terhadap beberapa pertanyaan berikut.

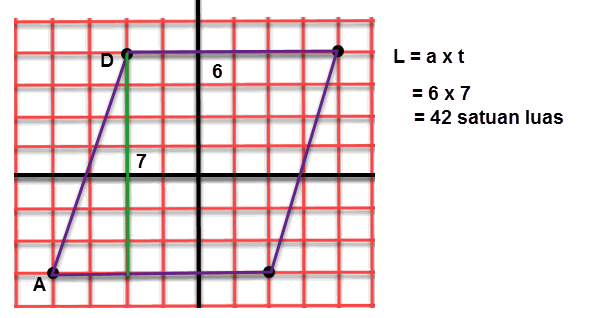
1. Beberapa koordinat titik pada bidang koordinat dapat membentuk bangun datar. Misalkan kita memiliki koordinat titik A(−4, −3), B(2, −3), C(4, 4), D(−2, 4). Bila titik-titik A, B, C, dan D dihubungkan, bangun apakah yang akan terbentuk? Jelaskan bagaiamana cara menentukan luasnya.
2. Diberikan 6 (enam) lingkaran dengan jari-jari r dalam sebuah daerah trapesium ABCD sama kaki dan panjang AD = 5r. Buktikan bahwa luas daerah yang diarsir adalah 6r² (6 − π).
Diketahui trapesium ABCD samakaki
Jari-jari = r
Panjang OD = 4r
Panjang DC = 6r
Panjang AD = 5r
Ditanyakan : Bukti daerah yang diarsir pada daerah trapesium
ABCD = 6r² (6 − π)
Karena ABCD adalah trapesium sama kaki maka <AOD adalah 90
Dengan menggunakan dalil pytagoras diperoleh
LABCD adalah trapesium samakaki, luasnya adalah
LABCD = AO x OD x OD
= 3r x 4r x 6 r x 4r
= 12r² + 24 r²
= 36r²

Luas 6 buah lingkaran yang jari r = 6πr²
Luas daerah yang diarsir= luas trapesium - luas lingkaran
= 36 r² -6πr²
= 6r²(6-n)