Keliling belahketupat didapat dari 4 kali sisi, sedangkan luas belahketupat adalah setengah hasil kali diagonal-digonal bangun tersebut. Keliling trapesium didapat dari dua kali jumlah sisi sejajar dengan jumlah sisi-sisi lainnya, sedangkan luas layang-layang adalah setengah dari hasil kai kedua diagonalnya. Berikut ini penjelasan mengenai keliling dan luas belahketupat dan layang-layang.
| No | Pertanyaan | Jawaban | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Jika d₁ dan d₂ merupakan diagonal-diagonal kedua belahketupat, maka lengkapilah gambar di atas | a. Simpulkan hubungan antara panjang sisi s dengan keliling Keliling belahketupat didapat dari 4 kali sisi. b. Jelaskan bagaimana cara menemukan rumus luas belahketupat (dengan menggunakan konsep luas persegi atau persegi panjang). Perhatikan gambar belahketupat berikut | ||||||||||||
Langkah-langkah menemukan rumus luas jajargenjang adalah sebagai berikut.
Luas belahketupat = luas persegipanjang ACFG = panjang × lebar = AC × CF = AC × 1/2 BD Luas trapesium = 1/2 × d₁ × d₂ Sedangkan keliling belah ketupat, K = AB + BC + CD + AD = 4AB Secara umum dapat disimpulkan: Sebuah belahketupat dengan panjang sisinya a, maka luas dan keliling belahketupat adalah:
K = 4a L adalah luas belahketupat ABCD dan K adalah keliling belahketupat ABCD. d₁ adalah diagonal pertama dan d₂ adalah diagonal kedua. | ||||||||||||||
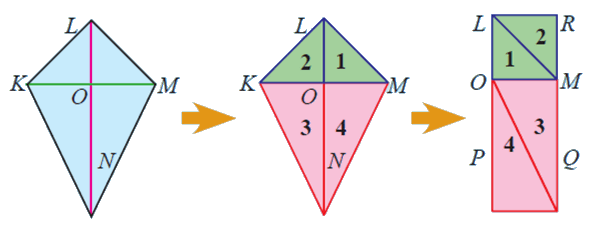
| 2. | Jika d₁ dan d₂ merupakan diagonal-diagonal kedua layang-layang, maka lengkapilah gambar. | Simpulkan hubungan antara panjang sisi a dan sisi b dengan keliling Keliling layang-layang didapat dari dua kali jumlah sisi sejajar dengan jumlah sisi-sisi lainnya. Jelaskan bagaimana cara menemukan rumus luas layang-layang (dengan menggunakan konsep luas persegi atau persegipanjang). Perhatikan gambar layang-layang berikut | ||||||||||||
Langkah-langkah menemukan rumus luas jajargenjang adalah sebagai berikut.
Luas layang-layang = luas persegipanjang LPQR = panjang × lebar = LP × PQ
Secara umum dapat disimpulkan: Sebuah belahketupat dengan panjang sisinya a, maka luas dan keliling belahketupat adalah:
d₁ adalah diagonal terpanjang dan d₂ adalah diagonal terpendek. L adalah luas layang-layang dan K adalah keliling. | ||||||||||||||
| 3. | Apakah belahketupat termasuk layang-layang? Jelaskan. Belahketupat dapat dikatakan layang-layang, karena semua sifat-sifat layang-layang terdapat juga pada sifat-sifat belahketupat | |||||||||||||
| 4. | Apakah layang-layang termasuk belahketupat? Jelaskan Layang-layang tidak dapat dikatakan belahketupat, karena ada sifat belahketupat tidak dimiliki sifat pada layang-layang, contoh sifat belah ketupat panjang sisinya semuanya sama. | |||||||||||||
Ayo Kita Mencoba
Contoh 1 :
Belahketupat PQRS memiliki panjang diagonal masing-masing 10 cm dan 15 cm. Tentukan luas belahketupat PQRS tersebut!
Dari kegiatan mencari luas belahketupat, diperoleh aturan sebagai berikut.
| L= | 1 | d₁ x d₂ |
| 2 |
| L= | 1 | 10 x 15 = 75 |
| 2 |
Contoh 2 :
Misalkan ABCD sebuah belahketupat dengan luas 24 cm². Dan panjang AD = 5 cm
Panjang OC = x cm dan OD = y cm, dan nilai x + y = 7.
Hitunglah
a. Keliling belahketupat ABCD.
Karena setiap sisi belahketupat sama panjang dan AD = 5 cm, maka keliling belahketupat ABCD adalah 4 × 5 = 20 cm.
b. Panjang diagonal-diagonalnya
| L= | d₁ x d₂ |
| 2 |
| 24 = | 2x x 2y |
| 2 |
⇒ xy = 12
Karena xy = 12 dan x + y = 7, maka x dan y yang memenuhi adalah x = 3 dan y = 4.
Jadi, panjang AC = 2 × OC = 2 × 3 = 6 cm
Panjang BD = 2 × OD = 2 × 4 = 8 cm
Ayo Kita Berlatih
1. Tentukan ukuran diagonal-diagonal suatu belah ketupat yang memiliki luas 48 cm²!
Luas belah ketupat= 1/2. d₁. d₂
48= 1/2 d₁ . d₂
48x2=1/2 x 2 .d₁. d₂
96 = d₁. d₂
Jadi bisa kita ketahui kalau diagonal diagonalnya adalah faktor dari 96 yaitu angka yang mungkin adalah 1 dan 96, 2 dan 48, 3 dan 32, 4 dan 24, 6 dan 16, 8 dan 12
2. Diketahui layang-layang ABCD mempunyai luas 1.200 cm². Selain itu, ada layang-layang PQRS yang masing-masing panjang diagonalnya dua kali panjang diagonal-diagonal layang-layang ABCD. Tentukan luas layang-layang PQRS!
3. Diketahui panjang diagonal layang-layang HIJK adalah 8 cm dan 12 cm. Tanpa menggunakan penggaris, buatlah gambar layang-layang HIJK tersebut. Bandingkan hasilnya dengan layang-layang HIJK yang dibuat dengan penggaris!
Lebih baik pakai penggaris
4. Tiga persegi masing-masing panjang sisinya 6 cm, 10 cm dan 8 cm ditempatkan seperti pada gambar di bawah. Tentukan luas daerah yang diarsir.
Persegi adalah bidang dengan batas ungu dengan ukuran 6 x 6
Persegipanjang adalah bidang dengan batas merah dengan ukuran 18 x 10
Segitiga I adalah bidang warna kuning dengan alas 16 cm dan tinggi 6 cm
Segitiga II adalah bidang warna biru dengan alas 18 x 10
Sehingga
5. Bangunan di bawah ini mempunyai empat sisi yang kongruen dan luasnya adalah 132 cm². Carilah kelilingnya.
Luas = P x L = 132 cm².
L=11 x 12 = 132 cm².
K= 2(P+L) = 2(11+12)
K = 46 cm
6. Perhatikan gambar trapesium berikut.
a. Tentukan nilai x. Nilai x = 70°
b. Tentukan nilai y. Nilai y = 110°
c. Tentukan luas trapesium di samping. L = 280 cm²
7. Perhatikan gambar berikut.
PQRS adalah jajargenjang, dengan panjang TR = 22 cm, PQ = 7 cm, dan QR = 25 cm. Panjang PT adalah ….
8. Diketahui belah ketupat ABCD dan BFDE dengan BD = 50 cm dan AE = 24 cm, dan EF = 2 × AE. Luas daerah yang diarsir adalah ....
9. Diketahui jajargenjang ABCD. Titik P dan Q terletak pada AC sehingga DP dan BQ tegak lurus AC. Jika panjang AD = 13 cm, AC = 25 cm dan luas jajargenjang tersebut adalah 125 cm², maka panjang PQ adalah ... cm
10. Diketahui luas suatu trapesium adalah 60 cm². Jika hasil pembagian panjang sisi-sisi sejajarnya adalah 3/5 cm, dan tinggi trapesium 15 cm, tentukan panjang masing-masing sisi sejajar tersebut.
⇒a:b = 3:5
Luas = a+b/2 x t
60 = a+b/2 x 15
60 = a+b x 7,5
8 = a+b
a = 3/8 x 8 = 3
b = 5/8 x 8 = 5
Jadi, a = 3 dan b = 5
11. Diketahui jajar genjang ABCD dengan titik E dan F merupakan titik tengah garis AB dan CD. Tarik garis AF, BF, DE, dan CE. Bentuk segiempat apakah yang terbentuk ditengah-tengah jajar genjang tersebut? Jelaskan jawabanmu!
Segiempat yang terbentuk adalah jajargenjang
12. Diketahui jajargenjang ABCD. Titik P dan Q terletak pada AC sehingga DP dan BQ tegak lurus AC. Jika panjang AD = 13 cm, AC = 25 cm dan luas jajargenjang tersebut adalah 125 cm², maka panjang PQ adalah ... cm (sama dengan nomor 9)
13. Diketahui panjang salah satu diagonal belahketupat 48 cm. Bila keliling belahketupat 100 cm, maka tentukan luas belahketupat tersebut.
Diketahui :
Kelliling = 4 x sisi
100 = 4s, s =100/4 = 25 cm
1/2 d₁ = 48/2 =24 cm
Kita cari adalah diagonal yang satu lagi sehingga
1/2 d₂² = s² - 1/2 d₁²
1/2d₂² = 25² - 24²
menurut Tripel phytagoras 7, 24, 25
maka 1/2d₂ = 7 cm
d₂ = 14 cm
L belahketupat = d₁ x d₂ /2
48 x 14 /2= 336 cm²
14. Diketahui trapezium ABCD siku-siku di B dengan panjang AB = 18 cm, CD = 20 cm, dan luasnya 108 cm². Hitunglah keliling trapesium ABCD tersebut.
Keliling trapesium ABCD tersebut = 50 cm
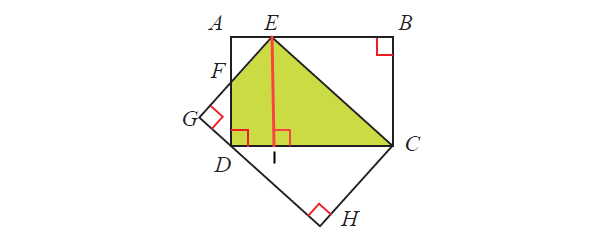
15. Perhatikan gambar berikut !
Diketahui ABCD dan CEGH adalah dua persegipanjang kongruen dengan panjang 17 cm, dan lebar 8 cm. Titik F adalah titik potong sisi AD dan EG. Tentukan luas segiempat EFDC !
Kita tarik garis dari titik E tegak lurus terhadap DC.. misalnya titik potongnya adalah I
Panjang CI dapat dicari dengan pythagoras yaitu 15 cm
Sehingga panjang AE = 2 cm
Misal AF = x maka FD = 8 - x
Karena FD = FE maka
(8 - x)² = 2² + x²
64 - 16x + x² = 4 + x²
60 = 16x
x = 15/4 = 3,75
Sehingga FD = 8 - 3,75 = 4,25
Bangun EFDC merupakan bangun layang layang
Jadi luas arsir = luas layang layang = 2 x luas segitiga CDF
Luas arsir = 17 x 4,25 = 63,75 cm²
Jawabannya 72,25






















0 komentar:
Post a Comment
Mohon tidak memasukan link aktif.