Luas dan Volume Balok serta Prisma Segi Banyak

Heksahedron adalah bangun ruang yang dibatasi enam permukaan (sisi). Jikas sisi-sisi terbentuk dari tiga pasang persegi panjang yang kongruen heksahedron tersebut dinamakan balok. Jika sisi-sisinya terbentuk dari tiga pasang persegi yang kongruen heksahedron tersebut dinamakan kubus. Pada tulisan ini saya mencoba untuk menemukan luas permukaan dan volume dari heksahedron dan prisma segi banyak, menghitung luas permukaan heksahedron dan prisma segi banyak. dan menentukan rumus luas permukaan heksahedron dan prisma segi banyak.

1. Luas Permukaan dan Volume Balok
Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi panjang, dengan paling tidak satu pasang diantaranya berukuran berbeda. Luas pemukaan balok adalah jumlah luas seluruh permukaan (bidang) balok. Apabila sisi-sisi balok direbahkan akan terbentuk jaring-jaring balok maka luas jaring-jaring balok itulah yang disebut sebagai luas permukaan balok. Atau dengan kata lain jumlah semua luas sisi balok dinamakan luas permukaan balok.

Balok mempunyai 6 sisi yang berbentuk persegi panjang. Persegi panjang-persegipanjang tersebut dapat dihitung luasnya dengan mengalikan panjang dan lebarnya. Hitunglah luas semua sisi balok kemudian jumlahkan semua luas sisi balok yang kamu peroleh. Balok mempunyai enam sisi yaitu Luas sisi alas = luas sisi atas, luas sisi depan = luas sisi belakang, dan luas sisi kanan = luas sisi kiri. Sehingga luas permukaan balok dapat dituliskan sebagai berikut :

Luas Permukaan Balok = 2 pl + 2 pt + 2 lt atau 2 (pl+pt+lt)

Contoh soal :

Sebuh balok berukuran panjang 18 cm, lebar 12 cm, dan tinggi 10 cm. Hitunglah luas permukaan balok tersebut?
Penyelesaian :
Diketahui : Panjang = 18 cm, Lebar = 12 cm, dan Tinggi = 10 cm. Ditanya : Luas permukaan balok?
Jawab :
Luas permukaan balok = 2 (pl+pt+lt)
= 2 (18 x 12) + (18 x 10) + (12 x 10)
= 2 (216 + 180 + 120)
= 2 x 516 cm²
= 1.032 cm²
Jadi, luas permukaan balok adalah 1.032 cm²

Volume Balok
Volume balok dapat ditemukan menggunakan kubus satuan. Susunan mula-mula yang dapat dikatakan sebagai alas balok. Kemudian menumpukkan kubus-kubus satuan di atasnya sampai beberapa tingkat. Banyak kubus satuan pada setiap tingkat adalah sama.  Banyak kubus satuan yang dapat disusun pada sebuah balok dinamakan volume balok.

Volume balok dapat dihitung dengan menyusun kubus satuan cm³ pada balok. Kubus satuan cm³ yaitu kubus yang panjang rusuknya 1 cm.

Banyak kubus satuan pada dasar balok sebagai panjang dan lebar
Banyak tingkat kubus satuan pada balok sebagai tinggi balok

Banyak kubus satuan pada balok = Volume balok = panjang x lebar x tinggi

Contoh Soal :
Suatu balok panjangnya 10 cm, lebar 8 cm, dan tinggi 6 cm. Berapakah volume balok tersebut?
Penyelesaian:
Volume balok = p x l x t = 10 cm x 8 cm x 6 cm = 480 cm³

2. Luas Permukaan dan Volume Prisma Segi Banyak
Untuk menghitung luas permukaan prisma segi banyak dapat dilakukan dengan cara menghitung semua sisi prisma. Tuliskan semua sisi prisma kemudian hitunglah luas masing-masing sisi. Hitung juga luas permukaan prisma, yaitu jumlah luas semua sisi prisma. Luas permukaan prisma juga dapat ditentukan dengan menghitung luas jaring-jaring prisma.

Luas Selimut Prisma
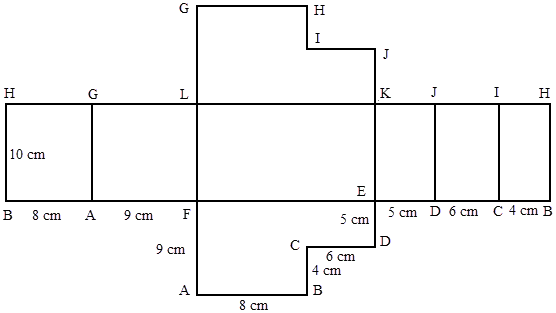
Pada jaring-jaring prisma tampak bahwa gabungan sisi tegak prisma berbentuk persegi panjang yang disebut selimut prisma. Panjang selimut prisma sama dengan jumlah panjang rusuk alas prisma dan lebar selimut prisma sama dengan tinggi prisma.
Panjang selimut prisma = 8 + 9 + 14 + 5 + 6 + 4 = 46 cm (14 diperoleh dari 8 + 6)
Lebar selimut prisma = 10 cm
Luas selimut prisma = 46 x 10 = 460 cm²

Luas Sisi Alas dan Sisi Atas
Sisi alas prisma sama dan sebangun dengan sisi atas prisma. Artinya, luas sisi alas sama dengan luas sisi atas.
Luas Sisi Alas = (14 x 9) - (6 x 4) = 126 - 24 = 102 cm²
Luas Sisi Alas dan Sisi Atas = 2 x 102 = 204 cm²

Luas permukaan prisma = 460 cm² + 204 cm² = 664 cm²

Secara umum rumus luas permukaan prisma dapat dituliskan sebagai berikut.
Luas = 2 x luas alas + keliling alas x tinggi

Volume Prisma Segi Banyak
Selain balok, volume prisma pada umumnya dapat ditentukan dengan menghitung banyak kubus satuan. Alas prisma di atas berbentuk segi enam. Banyak kubus satuan yang dapat dimuat pada alas prisma sama dengan luas alas prisma.
Banyak kubus satuan pada alas prisma = 102
Banyak tingkat kubus satuan pada prisma = 10
Banyak kubus satuan pada prisma = 102 x 10 = 1.020
Volume prisma = 1.020 cm³

Banyak kubus satuan pada alas prisma sama dengan luas alas prisma. Banyak tingkatan kubus satuan pada prisma sama dengan tinggi prisma. Oleh karena itu, volume prisma dapat dituliskan dalam rumus berikut.

Volume Prisma = luas alas x tinggi = L_alas x t

Soal Latihan (Hal. 122 Tema 6 sub tema 3)
1. Pak Heri membuat wadah pakan ternak dari seng. Wadah tersebut berbentuk prisma tanpa tutup dengan bentuk alas di bawah. Tinggi wadah 8 cm.
a. Berapa luas seng yang diperlukan?
Karena pakan ternak tanpa tutup maka hanya dihitung sisi alasnya saja.
Panjang selimut = 52 + 18 + 60 + 38 + 8 + 20 = 196 cm²
( angka 8 dari 60-52, dan angka 20 dari 38-18)
Lebar selimut = 8 cm (tinggi wadah)
Luas selimut = 196 x 8 = 1.568 cm²
Luas alas = (60 x 38) - (52 x 20) = 2.280 - 1.040 = 1.240 cm²
Luas permukaan wadah = 1.568 cm²+ 1.240 cm² = 2.808 cm²


b. Berapa volume wadah?
Volume wadah = Luas alas x tinggi = 1.240 x 8 = 9.920 cm³

2. Pak Siswanto seorang tukang kayu. Ia membuat sebuah peti untuk menyimpan peralatan kerjanya. Peti berbentuk balok dengan panjang 80 cm, lebar 25 cm, dan tebal 5 cm. Pak Siswanto hendak mengecat seluruh permukaan peti tersebut. Berapa luas permukaan peti yang harus dicat Pak Siswanto?

Luas Permukaan Balok = 2 (pl+pt+lt) = 2((80x25)+(80x5)+(25x5) = 2(2.000+400+125))
= 2 x 2.525 = 5.050 cm²

3. Paman Rustam membuat dua akuarium, yaitu akuarium A dan B dengan bentuk dan ukuran sebagai berikut.
A = 15 x 8 x 12
B = 20 x 9 x 9
a. Berapa luas kaca diperlukan untuk membuat dua akuarium tersebut?

Luas Permukaan A = 2 (pl+pt+lt) = 2((15x8)+(15x12)+(8x12) = 2(120+180+96))

= 2 x 396 = 792 cm²

Luas Permukaan B = 2 (pl+pt+lt) = 2((20x9)+(20x9)+(9x9) = 2(180+180+81))

= 2 x 441 = 882 cm²
Jumlah A dan B =792 + 882 = 1.674 cm²

b. Berapa volume air yang dapat ditampung dalam akuarium A?
Volume A = p x l x t = 15 x 8 x 12 = 1.440 cm³